Estimating Foundation Settlement from Field Soil Tests

This article presents various methods of measuring foundation settlement from the result of field/ in-situ soil testing.

Settlement estimation is a critical aspect of geotechnical engineering, especially in construction projects where the stability and longevity of structures are paramount. Understanding how the soil beneath a structure will behave under load is essential for ensuring the safety and durability of buildings, bridges, roads, and other infrastructure.

Aside the analytical methods of estimating foundation settlement, which was covered in an earlier article, there are still several methods by which foundation settlement can be estimated directly from soil tests using empirical equations. These aspects of settlement evaluation are well covered in Annexes of Eurocode 7 (Part 2).

In this article some of the in-situ methods of evaluating foundation settlement and their corresponding empirical equations will be presented.

Types of Field Soil Tests

Field soil tests encompass various techniques designed to assess the properties and behaviour of soil in-situ, that is directly on project site. A separate article has been presented on this. (See: Field Methods of Measuring Soil Bearing Capacity). Some of the most common field test that can be used to determine settlement of soils include the following:

Standard Penetration Test (SPT)

The Standard Penetration Test (SPT) (Figure 1) is one of the most basic methods of estimating foundation settlement. During a typical SPT, a hollow sampling tube is driven into the soil at the test location using a standard weight dropped from a standard height (Figure 1). The number of blows required to advance the sampler a specified distance is recorded as the Standard Penetration Resistance or N-value. This N-value reflects the soil’s resistance to penetration and offers an indication of its relative density and cohesion. Lower N-values often suggest softer, more compressible soils that may undergo higher settlement under loading.

Having obtain the N-values, empirical correlations between SPT N-values and foundation settlement can be utilized to compute the expected settlement of any foundation that is to be founded in the underlying soil.

Plate Load Test

In this test, a large steel plate (Figure 2) is placed on the ground surface at the test location, and a known load is incrementally applied to the plate using hydraulic jacks or loading frames. The settlement of the plate under the applied load is measured at regular intervals using dial gauges or electronic displacement transducers. This settlement data provides valuable insights into the soil’s compressibility and its ability to support foundation loads.

Therefore, using the plot of applied pressure versus settlement, the actual or limiting settlement of a proposed foundation in a given soil mass can be evaluated by correlating pressure with settlement.

Pressure-meter Test

During a pressure meter test, a cylindrical probe equipped with pressure sensors is inserted into a borehole drilled at the test location (Figure 3). The probe is then inflated using water or gas, exerting pressure against the surrounding soil. The pressure required to inflate the probe and the corresponding volume change of the soil are measured continuously throughout the test at various depths within the borehole.

An analysis of the pressure-volume relationship obtained from the Pressure meter Test, allows us to derive valuable information about the soil’s stiffness, strength, and compressibility. This data can then be used to accurately predict foundation settlement under different loading conditions by using empirical equations.

This test involves inserting a cylindrical probe into the ground and pressurizing it. The pressure required to expand the probe against the soil provides information about soil stiffness and strength.

Field Tests and Foundation Settlement

Once the necessary field soil tests are conducted, engineers use empirical correlations, analytical methods, or numerical modelling to estimate settlement. Some common approaches include:

Empirical Correlations: Engineers often rely on established correlations between field test results and settlement behaviour. These correlations are based on historical data and empirical relationships derived from laboratory and field observations.

Analytical Methods: Analytical methods, such as the theory of elasticity and consolidation theory, are employed to predict settlement based on soil properties and loading conditions. These methods involve mathematical modelling and typically require simplifying assumptions about soil behaviour.

Numerical Modelling: Finite element analysis (FEA) and finite difference methods (FDM) are numerical techniques used to simulate the behaviour of soil under loading conditions. By discretizing the soil mass into small elements, these methods can provide detailed insights into settlement patterns and deformation.

This article is concerned with the empirical correlations only. Some of these correlations are presented below for the aforementioned field tests.

Terzaghi & Perks Method (SPT)

Terzaghi and Peck (1967) were the first to propose a rational method for predicting the settlement of a shallow foundation in granular soil. They established a relationship between the elastic settlement of a square foundation (denoted as S_e, foundation) with a width of B and the settlement of a 300 mm wide square plate (S_e, plate) subjected to the same pressure.

S_{e,fdn}=S_{e,plate}\times(\frac{2B}{B+0.3})^2 (1-\frac{1}{4}\frac{D_f}{B})

Where: B and D_f are the width and depth of the foundation respectively

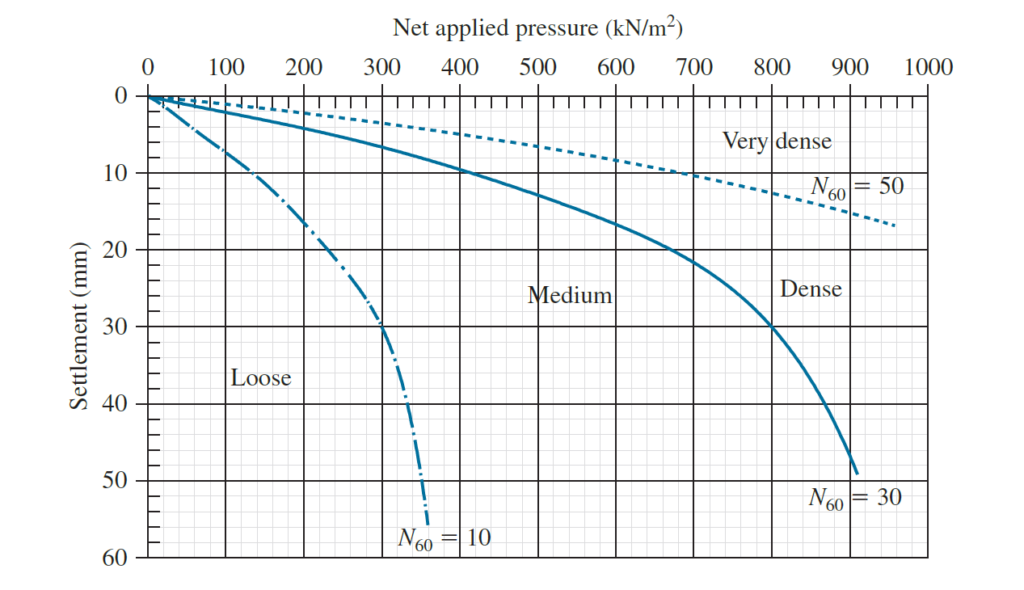
In the above equations, the final term accounts for the reduction in settlement as the foundation depth increases. Leonard’s (1986) recommended substituting 1/4 with 1/3, based on additional load test data. The values of S_e, plate can be obtained from Figure 4, which summarizes the plate loading test data provided by Terzaghi and Peck (1967). These load tests were conducted on thick deposits of normally consolidated drained sand. Although originally proposed for square foundations, this method can be cautiously applied to rectangular and strip foundations. Any deeper influence zone and increased stresses within the underlying soil mass in the case of rectangular or strip foundations are counterbalanced by the rise in soil stiffness.

Biraud Method (Pressure-meter Test)

Biraud (2007) proposed a method based on pressure-meter tests from which the load-settlement diagrams of foundations can be derived. A detailed explanation of the procedure is beyond the scope of this article. However, the following is a step-by-step procedure for performing the analysis.

Step 1: Conduct pressure meter tests at different depths in the chosen location. Record the pressure inside the measuring device for cavity expansion (referred to as pp) and the increase in cavity radius (DRyRo) at each depth.

Step 2: Extend the straight portion of the pressure meter test curve to zero pressure and adjust the vertical axis accordingly. Re-zero the DRyRo axis.

Step 3: Create a strain influence factor diagram for the specific foundation being analyzed. Develop an average pressure meter test curve using data from all pressure meter tests within the depth of influence.

Step 4: Use the average pressure meter test curve to generate a plot of mean pressure (pp(m)) versus DRyRo.

Step 5: Utilize the mean pressure meter test curve to construct a load-settlement plot for the foundation. Use equations to calculate elastic settlement (S_e) based on known parameters such as foundation width (B) and load per unit area (q_o).

Step 6: Determine additional parameters needed for the calculations, such as shape factor (fL/B), eccentricity factor (f_e), load inclination factor (f_d), and slope factor (f_b, d).

Step 7: Prepare a table to organize the calculations, including columns for DRyRo, pp(m), S_e, S_eyB, G, and q_o.

Step 8: Complete the table by calculating SeyB from DRyRo values, determining Se using known parameters, obtaining G from a provided figure, and calculating q_o using an equation. Finally, plot a graph of S_e versus q_o based on the table data to determine the settlement magnitude for a given load.

For more on how to evaluate settlement in foundations, see referenced texts.

Plate Load Test

In the plate load test, the following correlations exist for verifying foundation settlement based on whether the soil is clay or sand deposit.

For clay soil:

S_f=S_p\frac{B_f}{B_p}

For Sandy soil:

S_f=S_p (\frac{2B_f}{B_f+B_p})^2

Where: S_f & S_p are the settlement of the foundation and plate respectively while B_f and B_p are the width of the foundation and plate respectively.

Worked Example

A 2.5 m square foundation placed at a depth of 1.5 m within a sandy soil applies a net pressure of 120kN/m² to the underlying ground. The sand has γ = 18.5kN/m3 and N₆₀ =25. What would be the settlement.

For net applied pressure = 120 kN/m2 and N₆₀ = 25; from Figure 4, S_e, _plate = 4 mm. Therefore:

S_{e,fdn}=S_{e,plate}\times(\frac{2B}{B+0.3})^2 (1-\frac{1}{4}\frac{D_f}{B})

S_{e,fdn}=4\times(\frac{2\times2.5}{2.5+0.3})^2 (1-\frac{1}{4}\frac{1.5}{2.5}) =10.2mm

Conclusion

Field soil tests are indispensable tools not just for assessing soil bearing capacity but for also evaluating foundation settlement in geotechnical engineering. With the use of by empirical equations and the result of field tests, engineers can make informed decisions about foundation design with respect to settlement.

Sources & Citations

• .M Das and N. Sivakugan (2019). Principle of Foundation Design. Ninth Edition, SI Edition
• Bond A and Harris A (2008) Decoding Eurocode 7. Taylor & Francis, London, UK.