Designing a Waffle Slab-Worked Example

Waffle slabs are not different from a ribbed slab, their design is indeed based on the same principle as the ribbed and troughed slab system. The only difference is that waffle slabs have ribs spanning both directions and as a result, they are often classified as two-way slab systems.

Also in contrast to ribbed slabs, waffle slabs tend to be dipper and are able to span longer areas. Although the topping in waffle slabs is thinner while the ribs are narrower than that of an equivalent ribbed slab. Waffle slabs may be supported by deep or wide-band beams or may be supported directly on columns. In each case, the slab has a solid cross-section at the support in order to resist the shear and punching stresses which tend to be critical at the supports.

Geometry

The average self-weight of a waffle slab can be determined from expression 1 using figure 1. or alternatively may be obtained from tables provided by mould specialists showing the mould dimensions against the estimated self-weight of the slab based on the spacing between ribs.

The waffle slab is formed through the use of special moulds, the dimensions can be obtained from a mould specialist, this includes the width, depth and volume of void per mould. Generally, the standard moulds are 225mm up to 425mm deep with toppings of 50mm – 100mm.

*Figure 1: Terms for estimating self weight of a waffle slab*

{ f}_{ s }=\frac { 25 }{ zy } \left\{ zyh-n\left[ \frac { s }{ 3 } \left( { a }^{ 2 }+{ b }^{ 2 }+\sqrt { { a }^{ 2 }{ b }^{ 2 } } \right) \right] \right\}

{ f }_{ s }= self\quad weight\quad of\quad floor\quad (kN/{ m }^{ 2 })\\ n=number\quad of\quad waffles

Analysis and Design

Contrary to common knowledge, a waffle slab ought to be analyzed and designed as a flat slab rather than a two-way restrained slab even though its behaviour is more of a two-way restrained slab. This is because the torsional stiffness of a typical waffle slab is considerably lower than the equivalent two way restrained slab. Hence, the coefficients for two way restrained slabs may overestimate the torsional restraints offered by the slab edges and might not be appropriate, especially where wide band beams are the preferred choice for beams . However, where the waffle slab is supported on beams which can be guaranteed to resist torsion at the corners, coefficients for two ways restrained slabs may be used. In the case of waffle slabs supported directly on columns, the slab must be analyzed and designed completely as a flat slab.

As with one way ribbed slabs, the ribs in waffle slabs are basically beams and the rules for beam design are followed. The section is designed as a solid section at the support (rectangular beam) and as a flanged section at the span. Light reinforcement or fabric mesh based on the minimum area of steel is provided in the topping to avoid cracking.

Worked Example

The waffle floor shown in figure 2a & b is required for a shopping mall building. Preliminary sizing of the floor has been carried out by selecting a suitable mould and the slab dimensioned as shown in the figures. The floor is to be constructed from C25/30 concrete and steel bars having a yield strength of 460mpa.

Shows a waffle slab section — *Figure 2b: Typical Section through Slab*

Guidance on sizing waffle slabs can be found in the concrete Centre publication: Economic concrete frame elements.

Actions

The size of the chosen mould is indicated in figure 2b, and the size of the components determined, therefore the actions on this floor can be determined.

Permanent Actions

a.\quad{ f}_{ s } =\frac { 25 }{ yz } \left\{ yzh-n\left[ \frac { s }{ 3 } \left( { a }^{ 2 }+{ b }^{ 2 }+\sqrt { { a }^{ 2 }{ b }^{ 2 } } \right) \right] \right\}

=\frac { 25 }{ 9.6\times 12 } \left( 9.6\times 12\times 0.525-(11.66\times 9) \right) \times \\ \left( \frac { 0.425 }{ 3 } \left( { 0.775 }^{ 2 }+{ 0.625 }^{ 2 } \right) +\sqrt { 0.23 } \right)

=8.36kN/{ m }^{ 2 }

b.finshes\quad \& \quad services\quad =1.5kN/{ m }^{ 2 }

Permanent\quad Actions\quad { g }_{ k }=8.36+1.5\\=9.86kN/{ m }^{ 2 }

Variable Actions

Imposed\quad loads(malls)\quad { q }_{ k }=4kN/{ m }^{ 2 }

Design Value of Actions

By inspection the permanent actions are less than 4.5 times the variable actions, therefore equation 6.10b of BS EN 1991-1-1 can be used.

{ n }_{ s }=1.35\xi { g }_{ k }+1.5{ q }_{ k }

=(1.35\times 0.925\times 9.86)+(1.5\times 4)\\=18.3{ kN }/{ m }^{ 2 }

There are wide beams along the column strip which can be designed to resist torsion at the slab corners. Hence, the slab can be designed as a two–way restrained slab.

The corner panels are more critical, hence only the design of this panel is presented in this post. You’re encouraged to complete the design of the other panels following the same procedure.

Flexural Design

The coefficients for two way restrained slab are used to obtain the critical moment and shear forces in the slab. For the corner panels, the coefficient used is that of two adjacent sides discontinuous.

\frac { { l }_{ y } }{ { l }_{ x } } =\frac { 12 }{ 9.6 } =1.25

coefficients=\quad -0.066\quad \& \quad 0.049

Negative Moment at Supports

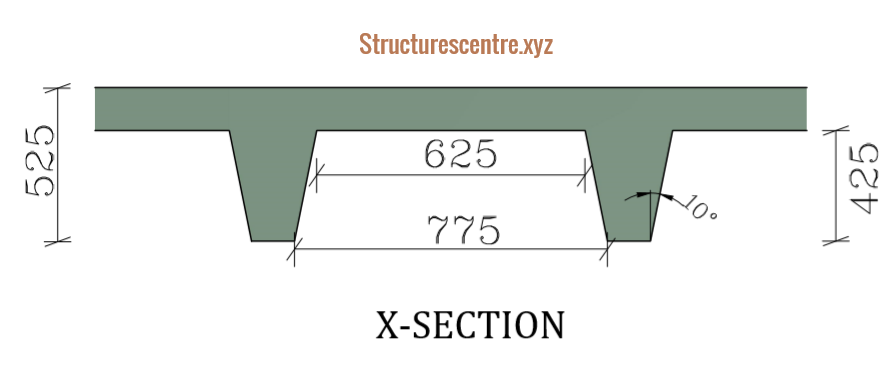
{ M }_{ Ed }=\left( 0.066\times 18.3\times { 9.6 }^{ 2 } \right) \times 0.9\\=100.2kN.m/ribs

Assuming the cover to reinforcement is 25mm and 12mm bars with 8mm links. The effective depth is

d=\left( h-{ c }_{ nom }+\frac { \phi }{ 2 } +links \right) \\=525-(25+12/2+8)=486mm

k=\frac { { M }_{ Ed } }{ { bd }^{ 2 }{ f }_{ ck } } =\frac { 100.2\times { 10 }^{ 6 } }{ 900\times { 486 }^{ 2 }\times 25 } =0.019

z=d\left( 0.5+\sqrt { 0.25-0.882k } \right) \le 0.95

=0.95d=0.95\times 486=461.7mm

{ A }_{ s }=\frac { { M }_{ Ed } }{ 0.87{ f }_{ yk }z } =\frac { 100.2\times { 10 }^{ 6 } }{ 0.87\times 460\times 461.7 } \\=542.3{ mm }^{ 2 }

Try\quad 5Y12/ribs\left( { A }_{ s,prov }=565{ mm }^{ 2 } \right) \\ Spread\quad across\quad effective\quad width\quad of\quad ribs

Positive Moment in Span

{ M }_{ Ed }=\left( 0.049\times 18.3\times { 9.6 }^{ 2 } \right) \times 0.9=\\74.38kN.m/ribs

Assuming the cover to reinforcement is 25mm and two layers of 12mm bars with 8mm links. The effective depth is

d=\left( h-{ c }_{ nom }+\frac { \phi }{ 2 } +{\phi}+links \right) \\=525-(25+12/2+12+8)\\=474mm

k=\frac { { M }_{ Ed } }{ { bd }^{ 2 }{ f }_{ ck } } =\frac { 74.38\times { 10 }^{ 6 } }{ 900\times { 486 }^{ 2 }\times 25 } =0.014

z=d\left( 0.5+\sqrt { 0.25-0.882k } \right) \le 0.95

=0.95d=0.95\times 474=450.3mm

{ A }_{ s }=\frac { { M }_{ Ed } }{ 0.87{ f }_{ yk }z } =\frac { 74.38\times { 10 }^{ 6 } }{ 0.87\times 460\times 450.3 } \\=412.74{ mm }^{ 2 }

Try\quad 4Y12/ribs\quad \left( { A }_{ s,prov }=452{ mm }^{ 2 } \right) \\ in\quad two\quad layers

Shear Design

{ V }_{ Ed }=\left( 0.49\times 18.3\times 9.6 \right) \times 0.9=77.5kN

{ V }_{ Rd,c }=0.12k\left( 100\rho { f }_{ ck } \right) ^{ \frac { 1 }{ 3 } }{ b }_{ w }d\ge { V }_{ min }

{ b }_{ w }=125+2cTan\theta =125+2\times 41Tan10\\=139.5mm

k=1+\sqrt { \frac { 200 }{ d } } =1+\sqrt { \frac { 200 }{ 486 } } =1.64<2

\rho =\frac { { A }_{ s } }{ { b }_{ w }d } =\frac { 226 }{ 139.5\times 486 } =0.0033\quad \\(assuming\quad 2H12)

{ V }_{ Rd,c }=0.12\times 1.64\left( 0.33\times 25 \right) ^{ \frac { 1 }{ 3 } }\cdot 139.5\times 486\\ =26.95kN

{ V }_{ min }=0.035{ k }^{ 3/2 }\sqrt { { f }_{ ck } } { b }_{ w }d

=0.035\times 1.64^{ 3/2 }\sqrt { 25 } \cdot 139.46\times 486=24.91kN

\left( { V }_{ Ed }>{ V }_{ Rd } \right) \quad \left( 77.5>26.96 \right)

Hence\quad shear\quad rebar\quad is\quad needed

Shear Reinforcement

\theta =0.5{ sin }^{ -1 }\left( \frac { { 5.56V }_{ Ed } }{ { b }_{ w }d\left( 1-{ f }_{ ck }/250 \right) { f }_{ ck } } \right)

\theta =0.5{ sin }^{ -1 }\left( \frac { 5.56\times 77.5\times { 10 }^{ 6 } }{ 139.5\times 486\left( 1-25/250 \right) 25 } \right) \\=8.20^{ \circ }

cot\theta =6.94>2.5\quad therefore\quad cot\theta =2.5

\quad z=0.9d=0.9\times 486=437.4mm

\frac { { A }_{ sv } }{ { s }_{ v } } \ge \frac { { V }_{ Ed } }{ z{ f }_{ ywd }cot\theta } =\frac { 77.5\times { 10 }^{ 3 } }{ 437.4\times 460\times 2.5 } \\=0.15

max\quad spacing\quad { s }_{ v }=0.75d=0.75\times 486\\=364.5mm

Use\quad Y8-300mm\quad centres\quad (0.34)

Deflection Verification

Limiting (L/d)

\left[ \frac { l }{ d } \right] _{ limit }=N\cdot k\cdot F1\cdot F2\cdot F3

\rho =\frac { { A }_{ s,req } }{ { A }_{ c } }

=\frac { 412.74 }{ \left( 900\times 100 \right) +\left( 139.46\times 425 \right) } =0.0028

{ \rho }_{ o }={ 10 }^{ -3 }\sqrt { { f }_{ ck } } ={ 10 }^{ -3 }\sqrt { 25 } =0.005

N=\left[ 11+\frac { 1.5\sqrt { { f }_{ ck } } { \rho }_{ o } }{ \rho } +3.2\sqrt { { f }_{ ck } } \left( \frac { { \rho }_{ o } }{ \rho } -1 \right) ^{ \frac { 3 }{ 2 } } \right]

=\left[ 11+\frac { 1.5\sqrt { 25 } \cdot 5 }{ 2.8 } +3.2\sqrt { 25 } \left( \frac { 5 }{ 2.8 } -1 \right) ^{ \frac { 3 }{ 2 } } \right]

N=35.53

k=1.3(end\quad span)

F1=0.82\quad ;\quad F2=\frac { 7 }{ l } =\frac { 7 }{ 9.6 } =0.73

F3=\frac { 310 }{ { \sigma }_{ s } } \le 1.5

{ \sigma }_{ s }=\frac { { f }_{ yk } }{ { \gamma }_{ s } } \left[ \frac { { g }_{ K }+{ \psi q }_{ k } }{ { n }_{ s } } \right] \left( \frac { { A }_{ s,req } }{ { A }_{ s,pro } } \right) \cdot \frac { 1 }{ \delta }

=\frac { 460 }{ 1.15 } \left[ \frac { 9.86+0.6(4) }{ 18.3 } \right] \cdot \frac { 412.74 }{ 452 } =244.7Mpa

F3=\frac { 310 }{ 244.7 } =1.27

\left[ \frac { l }{ d } \right] _{ limit }=35.53\times 1.3\times 0.82\times 0.73\times 1.27\\=35.11

Actual (L/d)

{ \left[ \frac { l }{ d } \right] }_{ Actual }=\frac { span }{ effective\quad depth } =\frac { 9600 }{ 474 } \\=20.25

Since the limiting value of l/d is greater than the actual l/d therefore deflection is satisfied in this slab.

Detailing Requirements

Minimum Area of Steel

{ A }_{ s }=0.26\frac { { f }_{ ctm } }{ { f }_{ yk } } { b }_{ t }d\ge 0.0013{ b }_{ t }d

{ f }_{ ctm }=2.56Mpa

{ A }_{ s }=0.26\frac { 2.56 }{ 460 } \cdot { 10 }^{ 3 }\times 100\ge 0.0013\cdot { 10 }^{ 3 }\times 100 \\=144.5{ mm }^{ 2 }/m

Use\quad A142\quad Mesh\quad in\quad Topping

Crack Control

stress\quad in\quad bars\quad { \sigma }_{ s }=245Mpa

maximum\quad crack\quad width\quad =0.4mm\quad o.k

This concludes this design example. The detailing of the typical corner panel has been attached as a pdf file. You’re encouraged to complete the design of the other panels and finish up the detailing.

Worked-Example-on-Waffle-Slab-Details-1

You might also like Designing a Trough(Ribbed Slabs): Designing a Trough Slab-Worked Example.

THANK YOU FOR READING!!! COMMENT & SHARE THIS POST IF YOU LIKE IT.