Design Of Steel Elements in Axial Compression TO EC3

Unlike members in axial tension, when structural elements are subjected to axial compression, they become vulnerable to failure through instability as a result of their geometrical properties rather than their material properties. For instance, it is very common to experience a slender structural element, such as the one shown on the featured image, suddenly bow when subjected to a significant compressive action. This phenomenon is often known as instability and in any case the structural element is said to buckle.

Structural elements subjected to axial compressive actions, are often known as columns or struts, with the former term being usually applied to the relatively heavy vertical members that are used to support beams and slabs; struts are more commonly associated with compression members in braced frames, girders and trusses.

In the design of elements in axial compression, of interest are steel elements, particularly the open steel sections because they belong to the category of structural elements with geometrical properties considered to be highly susceptible to this failure mode due to their relatively high slenderness ratios. Hence, their design must not only take into account material strength of the member as with steel elements in axial tension, but must also consider its stability against buckling.

Design Principles

The design of a steel element in axial compression must prove the adequacy of the chosen section against direct compression as well as the occurrence of instability due to buckling. According to EC3, four types of verifications are generally required for a member subjected to uniform compression, viz a viz – compression resistance, flexural buckling, torsional buckling and flexural torsional buckling.

However, there are exemptions. Closed steel sections are generally immune to torsional buckling and torsional flexural buckling due to their geometry hence, they are only checked for compression resistance and flexural buckling. But for open sections, all verification must be carried out. Although for columns and struts using hot rolled I and H sections, torsional and flexural torsional buckling is very much unlikely to determine the resistance of the element against buckling. Therefore, except the trial section is a Tee, Angle or a Channel, torsional and flexural torsional buckling need not to be verified. Consequently, in this article, we’ll focus on compression resistance and flexural buckling resistance. For guidance on the verification of members in compression against torsional and flexural torsional buckling, please refer to section 6.3.1.4 of BS EN 1993-1-1.

Compression Resistance

According to Clause 6.2.1(4) of BS EN 1993-1-1, the resistance of a steel section against compression is verified by satisfying the following equation:

\frac { { N }_{ Ed } }{ { N }_{ c.Rd } } \le 1.0

Where: N_Ed is the design value of the compressive action and   N_c,Rd  is the design resistance of the compression member to uniform compression (clause 6.2.1.1(2)) defined as:

{ N }_{ c,Rd }=\frac { A{ f }_{ y } }{ { \gamma  }_{ M0 } } 

Where: A is the area of the member based on section classification; f_y is the yield strength of the steel based on element thickness; ℽ_M0 is the partial factor for the resistance of members subject to instability which is set as 1.0 in the U.K National Annex to EC3.

Flexural Buckling Resistance

To verify steel members in compression against flexural buckling, BS-EN 1993-1-1 applies a reduction factor to the design resistance of the steel section.

This is obtained from clause 6.3.1.1(1) and the verification is carried out by satisfying the expression:

\frac { { N }_{ Ed } }{ { N }_{ b.Rd } } \le 1.0

Where: N_b,Rd  is the design buckling resistance of the compression member (clause 6.3.1.1(1)) given as:

{ N }_{ b,Rd }=\chi \frac { A{ f }_{ y } }{ { \gamma  }_{ M1 } } 

Where: Χ is the reduction factor that takes into account the flexural buckling, ℽ_M1 is the partial factor for the resistance of members subject to instability which is set as 1.0 in the U.K National Annex to EC3.

\chi =\frac { 1 }{ \phi +\sqrt { { \phi  }^{ 2 }-{ \lambda  }^{ 2 } }  } \le 1.0

\phi =\left[ 0.5+\alpha \left( \lambda -0.2 \right) +{ \lambda  }^{ 2 } \right]

λ is the non-dimensional slenderness given as:

\lambda =\frac { { L }_{ cr } }{ i } \cdot \frac { 1 }{ 93.9\varepsilon  } \quad for\quad class\quad (1-3)

L_cr is the buckling length of the compression member about the relevant axis;  i is the radius of gyration about the relevant axis;  α is the imperfection factor and is found in table 6.3 of BS-EN 1993-1-1 which is read against sections buckling curve. These buckling curves are labelled a-d and are found in Clause NA.2.17 of NA to BS EN 1993-1-1. Selecting a buckling curve is dependent on the geometry of the trial section.

Design Steps

• Determine the design compressive action for the appropriate load case and load combination
• Select a trial section and classify the section according to section 5.5 of BS-EN 1993-1-1 of EC3, for guidance, see: Classification of Steel Sections. If section is class 4 refer to BS-EN 1993-1-5 or chose a section that is at least class 4
• Verify the resistance of the member to uniform compression
• Verify the resistance of the member to flexural buckling about both minor and major axis
• Adopt section if satisfactory, else change section.

Worked Example

The maximum compressive force in the diagonals of the warren steel girder shown in the figure below is N_Ed = 725kN. Assuming the girder is perfectly pin-jointed. Design the diagonals against axial compression using a SHS section in S355 steel.  Take actual length of diagonals =1.8m

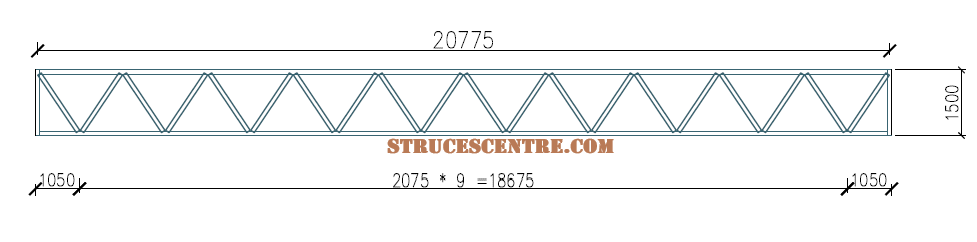
Try 90 x 90 x 8 Square Hollow Section (SHS)

Properties:

Depth, h=90mm; Width, b=90mm; Thickness, t= 8mm; Radius of gyration major axis i_yy =2.91cm; Radius of gyration minor axis i_zz =2.91cm; Area of section A = 25.6cm²

Section Classification

c=h-3t=90-3\left( 8 \right) =67mm

 \frac { c }{ t } =\frac { 67 }{ 8 } \le 33\varepsilon \quad \left( class\quad 1 \right) \quad =33\cdot \sqrt { \frac { 275 }{ 355 }  }

8.38<29\quad section\quad is\quad class\quad 1

Compression Resistance

{ N }_{ c,Rd }=\frac { A{ f }_{ y } }{ { \gamma  }_{ M0 } } =\frac { 2560\times 355 }{ 1.0 } =908.8kN

\frac { { N }_{ Ed } }{ { N }_{ c,Rd } } =\frac { 725 }{ 908.8 } =0.8\quad o.k

Flexural Buckling Resistance

Since the truss is pin-jointed, we can take the design length of the diagonals equal to the actual length = 1.8m

\lambda =\frac { { L }_{ cr } }{ i } \cdot \frac { 1 }{ 93.9\varepsilon  } =\frac { 1800 }{ 29.1 } \cdot \frac { 1 }{ 93.9\times \sqrt { \frac { 275 }{ 355 }  }  } \\=0.75

For hot finished SHS section, buckling curve a applies, hence α=0.21

\phi =\left[ 0.5+\alpha \left( \lambda -0.2 \right) +{ \lambda  }^{ 2 } \right] 

=\left[ 0.5+0.21\left( 0.75-0.2 \right) +{ 0.75 }^{ 2 } \right] =0.84

\chi =\frac { 1 }{ \phi +\sqrt { { \phi  }^{ 2 }-{ \lambda  }^{ 2 } }  } 

=\frac { 1 }{ 0.84+\sqrt { { 0.84 }^{ 2 }-{ 0.75 }^{ 2 } }  } =0.82\le 1

{ N }_{ b,Rd }=\chi \frac { A{ f }_{ y } }{ { \gamma  }_{ M1 } } 

=0.82\times \frac { 2560\times 355 }{ 1.0 } =745.2kN

 \frac { { N }_{ Ed } }{ { N }_{ b,Rd } } =\frac { 725 }{ 745.2 } =0.97<1\quad o.k

Adopt a 90 x 90 x 8 Square Hollow Section (SHS)

See: Design of Steel Elements in Tension to Eurocode

Citations

BS EN 1993: Design of steel structures – Part 1-1: General rules and rules for buildings

U.K National Annex to BS EN 1993: Design of steel structures – Part 1-1: General rules and rules for buildings

To download this article in pdf click here.

Thank You!