Derivation of Snow Loading to Eurocode 1

This article illustrates how to derive and apply snow loads to structures cited in areas prone to snow fall using Eurocode 1-1-3 and the U.K National Annex to Eurocode 1-1-4

In regions prone to heavy snow fall, snowfall can become so significant such that they constitute a load on structures. Therefore, if the aim of every structural design is to adequately capture all effect that may constitute a load on a structure, snowfall must be considered in areas where their effect is significant. And because snow loading only occurs in certain environments, there is no generic approach to derivation. There are a number of variations and conditions which a designer must be aware of when estimating snow loads.

Eurocode 1-1-3 provides a comprehensive set of guidelines for determining snow loads. However, since Snow loads are even more environmentally specific, a national annex must be utilized with the code depending on the country.

In this article, the UK National Annex will be utilized alongside the Eurocode 1-1-3 to illustrate how to derive snow loads on structures. It’s recommended that the reader gets a copy of the codes as a lot of references will be made to the code within this article.

Derivation Principle

In estimating snow load, there are two fundamental principles.  First, the designer is required make decisions regarding the structure’s form and the environment it is to be positioned in in order to calculate the snow load. Secondly, when estimating the size of the consequent persistent snow load onto the building, the possibility of snow accumulation must be taken into consideration.

To address the issues above, Eurocode 1 establishes a base load, factors are then applied to this base load to account for snowdrift. Hence to determine snow load two variables are required, the basic snow load which account for the environment and the shape factor which account for the form of the structure.

Basic Snow Load

The basic snow load (s_k) is defined as the quantity of snow on the ground at an altitude of 100 meters above mean sea level. Eurocode 1-1-3 Clause 1.6.1 establishes the likelihood of surpassing this number at 1 in 50 every year.

The basic snow load can be determine based on the expression given in Clause NA.2.8 of Eurocode 1-1-3 as:

s_k=[0.15+(0.1Z+0.05)+\frac{A-100}{525}

Where: Z is the zone number (i.e. 1, 2, 3) taken from the UK National Annex to Eurocode 1-1-3. A is the altitude factor; the ground level height of the location where the structure is located above mean sea level in meters. When examining locations near coastal regions that are less than 100m above mean sea level, the element of the expression having A is omitted.

Shape Factors

To accommodate for variations in snowfall thickness due to the geometry of roof structures, Eurocode 1-1-3 employs coefficient (μ₁) to adjust for geometric alterations. It is added to the basic snow load s_k and is determined by the kind of roof on the structure, whether flat, mono-pitch, duo-pitch, or multi-span. The closeness of protrusions, such as higher structural parts or chimney stacks, also impact on the value of form coefficient as would be seen in the next sections.

Shape Coefficient for Flat, Mono- & Duo-Pitch Roofs

For flat and single span pitched roofs, the shape coefficient μ₁ value is affected by the relative angle (α) of the roof pitch. Figure 5.1 of Eurocode 1-1-3 depicts this. The value of μ₁ for flat roofs is 0.8.

For mono-pitch roofs, the pitch angle is displayed against μ₁ in Figure 5.1 or Table 5.2 of Eurocode 1-1-3. For roofs with a pitch angle of 60° or greater, the value of μ₁ is accepted as 0.

In the case of dual-pitched roofs, the pitch angle of each side of the roof is measured against one. In the case of varying pitch angles, each portion of the roof will have its own distinct form coefficient. Before arriving at a final snow load under this circumstance, a succession of snow load patterns must be examined. The following patterns are usually considered:

• Both sides loaded with the 1 coefficient from Figure 5.1 or Table 5.2 for each side of the roof.
• Loaded on one side with NA Figure NA.2 and Table NA.1.
• Loaded the other side with NA Figure NA.2 and Table NA.1.

The constant snow load is regarded as the worst of the situations outlined above and should be considered for design. For further details, read Eurocode 1-1-3 Clause 5.3.3(3) and Figure 5.3. It is crucial to note that load scenarios (ii) and (iii) listed in Clause 5.3.3(4) have been superseded in the UK National Annex of Eurocode 1-1-3 by Clause NA 2.17.

Shape Coefficient for Multi-Span Roofs

When snow falls on multi-span roofs, the formation is not always uniform, hence determining the shape factor assumes an entirely different approach. To account for non-uniformity, the persistent snow load situation is determined using two loading conditions.

The first demands that the required coefficient be applied to the different pitches of each portion of the roof, in the same way as duo-pitched roofs were previously described.

The second condition permits snow to accumulate within the valley of the multi-span roof. The value of 1 for drifts occurring in valleys should be determined using Annex B2 of Eurocode 1-1-3.

Having considered the two loading conditions above, the shape factor is determined based on the lowest of the following equations:

\mu _1=\frac{2h}{s_k} \quad or \quad \frac{2b_3}{l_{s1}+l_{s2}}\quad or \quad 5

Figure B1 in Annex B of Eurocode 1-1-3 defines the variables listed above.

It is critical to note that these load instances are unique in that they are assessed in addition to the blanket snow load. For more information, see Clause B1(2) of Eurocode 1-1-3.

Shape Coefficients for Roofs Adjacent to Tall Structures

A peculiar scenario occurs when a roof is situated adjacent to or within 1.5m of vertical element, a barrier exist against which snow can build up. To address this issue, alternative coefficients, μ₁ & μ₃ need to be applied to the basic snow load separately.

The shape factor, μ₁ for flat roofs abutting taller structures is 0.8. The snowdrift that appears on top of the snow-covered roof is arrived out using the shape coefficients.

Figure 1 shows how the extent of the snowdrift is defined. It should be read in combination with Table B1 in Eurocode 1-1-3, which contains definitions for the variables listed. Snow loads indicated by recommendations given in Appendix B of Eurocode 1-1-3 are unusual and should not be considered in connection with the blanket snow load, as with snowdrift in multi-span roofs.

Shape Coefficients for Projections & Obstruction

Snow load is affected by small projections from the side elevation of structures, such as canopies, and impediments inside roofs, such as chimneys and parapets. They are barriers that allow snow to drift about and generate isolated heaping regions of snow. When analyzing snow loads on a building, shape codes representing increasing snow volumes are applied to the base load.

The reader is directed to Clause B4(1) and Figure B3 of Annex B of Eurocode 1-1-3 for the derivation of shape coefficient μ₁ for snowdrifts caused by obstructions such as chimneys. Clause B4(2)b of Eurocode 1-1-3 must be observed for canopies over entrances. This clause indicates that where more than 1m depth of snowdrift cannot occur, no shape factor must be used.

For smaller entrances less than 2m wide, the snowdrift’s depth ‘h’ is restricted to the lesser of the projection’s height or its breadth perpendicular to the wind direction.

Clause B4(2)c of Eurocode 1-1-3 defines the shape coefficient μ₁ for canopies as follows: μ₁= 2h / sk or 5, whichever is the lesser

For canopies over doors that do not project more than 5m, the value of μ₁ cannot exceed 2b / l_s1 with ‘b’ being the bigger of b1 and b2. Figure 2 illustrates the previously mentioned factors in further detail.

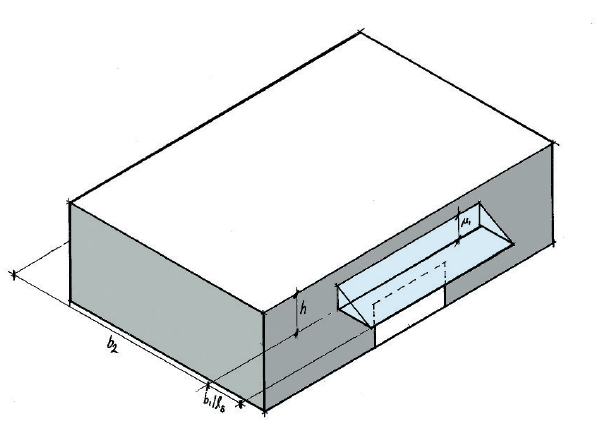
Clause B4(3) and Figure B4 of Eurocode 1-1-3’s Annex B. The snowdrift factor (1) is defined as the lowest of the following expressions:

\mu _1=\frac{2h}{s_k} \quad or \quad \frac{2b}{l_{s}}\quad or \quad 8

The drift length l_s might be 5h, b1, or a maximum of 15m. Figure B4 defines all of the variables specified in these expressions.

Partial Factors

Having estimated the value of snow load following the procedure discussed in the preceding section, the design value of the snow load must be determined. This is carried out through the application of partial factors.

 Snow loads are defined as variable fixed actions in Eurocode 1-1-3. The partial factors (q) for snow loads are determined by the chance of the Eurocode’s forecasted snowfalls actually happening. The loads on flat, mono-, and duo-pitched roofs are termed transient/persistent activities. All snow loads calculated using Annex B of Eurocode 1-1-3 are associated with extreme conditions and are thus designated as accidental actions (A_d).

Where snow load is considered in isolation, the partial factor 1.5γq is applied. However, when the snow load is considered in conjunction with other loads such as dead, imposed and wind, the partial factor for snow load is given as (0.2ψ1) 1.5γq.

Note:  γq is the partial factor for the snow load and ψ0 and ψ1 are the combination factors to be used when snow load is considered with others. The numbers stated adjacent to the factors above are their respective values. All snow loads must be considered in several combinations of dead, imposed and wind loads in order to create a worst-case condition.

Worked Example

An indoor sports hall is to be constructed adjacent to an existing further education college. It is located 1 km south of Inverness city centre and is 80m above mean sea level (Figure 3). Calculate the characteristic snow load on the roof and entrance canopy to the new sports hall. The roof pitch angle to the sports hall is 8°.

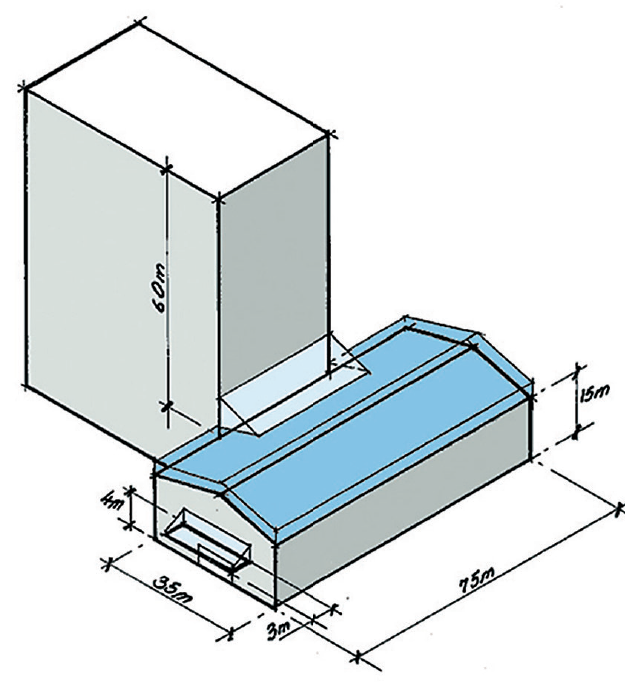
There are three snows loading that must be determined based on the configuration of the structure as shown in figure 3. First the snow load on the roof of the new sport hall. Secondly the snow load on the canopy at the entrance and finally snow drift to the hall roof due to the adjacent tall structure.

To begin, the first step is to derive the basic snow load using the figure in NA.1; Z = 4

s_k=[0.5+(0.1Z+0.05)+\frac{A-100}{525}

=[0.15+(0.1\times 4+0.05)+\frac{80-100}{525}\\=0.56kN/m^2

Snow Load on Roof of New Hall

To determine the overall snow load for the duo pitch roof for the new sports hall, we apply the shape factors. And since the roof slope is less than 8 deg. Therefore, shape factor μ₁ = 0.8

Therefore, snow load on sport hall roof:

= 0.56\times 0.8 =0.45kN/m^2

Snow Load on Canopy

For the canopy entrance, the shape factor will be determined using Clause B4(2)b in Eurocode 1-1-3 as said earlier in the article.

\mu _1=\frac{2h}{s_k} \quad or \quad 5

=\frac{2\times3}{0.56} =10.71>5

\mu _1=5

Therefore, snow load on canopy:

0.56\times 5 =2.8kN/m^2

Snow Drift due to Adjacent Tall Building

Table B1 in Eurocode 1-1-3 is used to determine the snowdrift load due to the adjacent existing structure which is significantly taller than the sport hall.

l_s =5 \times 60 =300m \le 30m \le15; l_e =15m

\mu _1=\frac{2h}{s_k} \quad or \quad \frac{2b}{l_{s}}\quad or \quad 8

\mu _1=\frac{2\times60}{0.56} \le \quad \frac{2\times35}{15}\le 8 =4.7

Thus, snow drift load on roof:

0.56\times 4.7 =2.6kN/m^2

Having determine these loads, they must be considered to act alongside other loads during the analysis and design of the structure after applying the appropriate partial factors. With respect to partial factors, only the snow load on the roof hall is considered as a variable static action and would require a partial factor of 1.5Q_k when considered in isolation with other actions. Whereas the snow load on the canopy as well as the snowdrift load are considered purely accidental actions, therefore should be treated as such when applying partial factors.

See: A Background to Extreme Loading Conditions

Sources & Citations

• Manual for the design of building structures to Eurocode 1 and Basis of Structural Design — Institution of Structural Engineers – April 2010
• BS EN 1991-1-3:2005. Eurocode 1: Actions on structures. Part 1-3: General actions – Snow actions. London, British Standards Institution, 2005
• UK NA to BS EN 1991-1-4:2011. National Annex to Eurocode 1: Actions on structures. Part 1-3: General actions – Snow Actions. London, British Standards Institution, 2001
• The Institution of Structural Engineers (2012) ‘Derivation of Snow Loading’, The Structural Engineer -Technical Guidance Note (level 3) 92(3), pp. 22-24