This article discusses the design intricacies of helical staircases. It offers an overview of the various methods of analyzing helical staircases and presents a method that can be used for preliminary analysis and design.

Helicoidal staircases, sometimes called helical staircases is another alternative solution for vertical circulation within constraint spaces. These unconventional staircases stand out as a fascinating and visually striking choice. They are an architectural marvel that combines functionality and aesthetic appeal. When designed properly, their graceful sweeping curve not only adds an elegant touch to a building’s interior but also presents the structural designer with a unique set of engineering challenges.
A helical staircase is very similar to a spiral staircase, however, while spiral staircases have a central support system, a helical staircase has no intermediate supports, and is only supported between floors. The consequence of having no intermediate support coupled with their unusual geometry is that the load and internal stress distribution within a helical staircase is very complex. In analyzing a helical staircase, the structure is treated like a space member, i.e. several internal forces come into play, therefore an interaction between the internal forces must be considered.
This article discusses the design intricacies of helical staircases. It offers an overview of the analysis of helical staircases and presents a method that can be used for preliminary analysis and design.
Analysis of Helicoidal Staircases
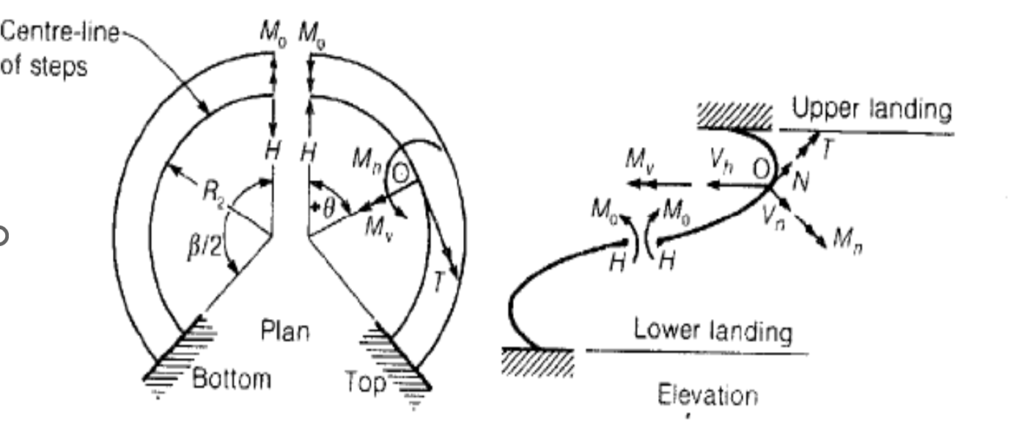
Perhaps the biggest challenge with designing a helical staircase is how to determine the internal forces. Unlike the traditional staircases which can be idealized as plane member, a helical staircase is a space frame, therefore can only be analyzed as a three-dimensional structure. Thus, for analysis purposes, the helicoidal surface is idealized such that the section consists of a warped surface which is generated by moving a straight line to touch a helix, so that the straight line is always normal to the axis of the helix (Figure 1). Up to 6 internal stresses can be found in a helical stair (Vertical moment; lateral moment; vertical shear; lateral shear; axial thrusts and torsion). All of these six internal actions would interact at any given section of the stair.
Because of this complexity in analyzing a helical stair, traditional analysis methods have simply been on various simplifications, idealization and assumptions. Several papers have been presented by researchers on the subject which can all be summarized into two basic approaches.
The first approach solves the analysis problem by transforming the helicoid into a fixed ended curved beam, so that the structure is now two-dimensional and can therefore be analyzed as a beam. This solution was proposed by Bergman (1956) and is known as the in-plane beam solution to the analysis of helical staircase.
In the second approach the helicoid is treated like a “helical girder” (a space structure). So that the helicoid is reduced to an elastic line with the same stiffness as the original structure. This solution is as per Morgan (1960).
Still on the need to discover an exact and even simpler method of analysis Santathadapom and Cusens (1966) attempted to simply the “helical girder” approach by publishing a list of design charts from which coefficients are determined. These coefficients are based on the geometrical properties of the helical stair and is applied in computing the value of the internal stresses within the stair. Further simplification of this work was done by Reynolds and Steedman (1988). Four design charts were published. These design charts today stand as ‘helical girder solution’ for helicoidal stairs.
As earlier stated, six internal forces occur in a helical staircase, and per Reynolds and Steedman, can be computed using the following equations:
Lateral Moment, Mn
Mn=M0SIN(θ)SIN(φ)-HR2θTAN(φ)COS(θ)SIN(φ)-HR2SIN(θ)COS(φ)+nR1sin(φ)(R1SINθ-R2θ)
Vertical Moment, My
My=M0COS(θ)+HR2θTAN(φ)SIN(θ)-NR12(1-COS(θ))
Axial Thrust, N
N=-HSIN(θ)COS(φ)-nR1θSIN(φ)
Torsion, T
T=(M0SIN(θ)-HR2θCOS(θ)TAN(φ)+nR12SIN(θ)-nR1R2θ)COS(φ)+HR2SIN(θ)SIN(φ)
Vertical Shear
Vn=nR1θcos(φ)-HSIN(θ)SIN(φ)
Radial Shear
Vh=HCOS(θ)
Where: Mo is the redundant moment acting tangentially at midspan; Mvs; is vertical support moments; H is the horizontal redundant force at midspan; n is design load on the staircase in (kN/m); R1 & R2 are the radiuses of the centerlines of loading and steps respectively; θx is the angle subtended in plan between the point at which the internal forces is to be determined and the midspan; Ø is the slope of tangent to the helix centerline measured from horizontal; and β or α is the total angle formed by the helical staircase in plan.
The redundant moment acting tangentially at midspan Mo; the horizontal redundant force H; and the vertical support moment Mvs are computed from the following equations respectively.
M_o=k_1n_sR_2^2
H=k_2n_sR_2
M_vs=k_3n_sR_2^2
Where: k1, k2 and k3 are coefficients obtained from chart.
The radius of the centerline of loading and steps, R1 & R2 can be computed from the following equations respectively.
R_1=\frac{2(R_o^3 - R_i^3)}{3(R_o^2-R_i^2)}R_2 =0.5(R_o+R_i)
Where: Ro and Ri is the outer and internal radiuses of the helical staircase in plan.
There are four charts with within Table 177 Reynold’s and Steedman Designer’s Manual from which the coefficients of k1, k2, and k3 are determined. Each of this chart covers a range of β of (30-360°) and Ø of (20-40°), a stair width: waste ratio of 5 and 10, and R1/R2 of 1.0 and 1.1. While this chart can not be taken as a one-size-fits all, these values fall within ranges of what would be frequently met in helical staircases design. Interpolations between the charts are also allowed in order to arrive at a more accurate values.
Finally, it must be noted that all the studies on the analysis of helical staircases (including the one presented in this article) that are based on either the curved beam or helical girder approach are all flawed. Why? Because they fail to take into account the 3-dimensional characteristics and the inherent structural efficiency of the helicoid. The implication is that the internal forces assumed for design can be sometimes far removed from reality. However, the advent of finite element analysis and the availability of software packages have steered in a more logical, exact and economical method of analyzing a helicoid. Therefore, except for preliminary analysis, helical staircases are best analyzed and designed using a FEA software.
Designing a Helicoidal Staircase
Having analyzed and determined the internal forces, designing the stair is pretty straightforward. There are six internal forces, each of which must be considered; design for flexure; design for shear and design for torsion. Also, because these forces act simultaneously, the interaction/ combined effect of them acting together should also be checked. The following steps is an overview of how to design a helicoidal stair
- Determine helical stair geometrical properties
- Estimate the design action on the helical stair
- Using the geometrical data and charts determine the values of the k1, k2 & k3 coefficients and compute the values of the redundant moment, vertical support moment, and horizontal redundant force.
- Compute the lateral, moment, vertical moments, axial thrust, lateral shear force, vertical shear force and torsion at different angles intervals.
- Design for flexure, using the maximum occurring values of the lateral & vertical moments.
- Design for shear using the maximum occurring values of the lateral and vertical shear
- Design for Torsion using the maximum occurring value of torsional moment.
Worked Example
An helicoidal staircase is required in the lounge of a proposed residential dwelling. The helicoidal staircase is to turn through an angle of 360°, have an angle of inclination of 20° to the horizontal and support a total permanent action and imposed action of 9.125kN/m2 and 1.5kN/m2 respectively. Estimate the internal forces in the helicoidal staircase at an interval of θ = 20° and determine the values for design, assuming the width of the staircase is 1.5 and the internal radius is 1.15m.
Actions
n_s =(1.35g_k+1.5q_k)\times b \\=(1.35\times9.125+1.5\times2.5)\times 1.5 \\=21.9kN/m
Geometry
R_i =1.15m
R_o =R_i+b\\=1.15+1.50=2.65mm
R_1=\frac{2(R_o^3 - R_i^3)}{3(R_o^2-R_i^2)} =\frac{2(2.65^3 - 1.15^3)}{3(2.65^2-1.15^2)}=2.0mR_2 =0.5(R_o+R_i)
=0.5(2.65+1.15)=1.9m
\frac{R_1}{R_2}=1.05; \quad \frac{b}{h}=6; \quad \beta=180\degree\quad \phi=25 \degree
Interpolating between the charts on Table 177 of Reynold’s and Steedman: Structural Engineers Designer’s Manual; we have:
k_1=-0.48
k_2=+2.45
k_3=-1.6
Analysis
Redundant Moment Acting Tangentially at Midspan
M_o=k_1n_sR_2^2
=-0.48\times21.9\times1.9^2\\=-37.9kN.m
Horizontal Redundant Force
H=k_2n_sR_2
=2.45\times21.9\times1.9\\=-101.7kN
Vertical Support Moment
M_{vs}=k_3n_sR_2^2=-1.6\times21.9\times1.9^2\\=-126.2kN.m
Having determined the values of Mo, H and Mvs, these values will be substituted into the internal forces’ equations, taking θ at an interval of 20°. This is summarized in the table below.
| S/n | θ (degrees) | Mn (kN.m) | T (kN.m) | My (kN.m) | N (kN) | Vn (kN) | Vh (kN) |
| 1.00 | 180.00 | -172.69 | -458.13 | -119.91 | -48.53 | 128.74 | 101.73 |
| 2.00 | 160.00 | -81.35 | -403.24 | -187.02 | -75.69 | 126.71 | 95.59 |
| 3.00 | 140.00 | 7.84 | -331.44 | -224.74 | -98.93 | 123.20 | 77.93 |
| 4.00 | 120.00 | 83.51 | -253.01 | -231.55 | -114.79 | 116.90 | 50.86 |
| 5.00 | 100.00 | 136.40 | -177.78 | -211.24 | -120.70 | 106.86 | 17.66 |
| 6.00 | 80.00 | 160.64 | -113.48 | -171.95 | -115.31 | 92.55 | -17.66 |
| 7.00 | 60.00 | 154.53 | -64.61 | -124.45 | -98.61 | 73.99 | -50.86 |
| 8.00 | 40.00 | 120.77 | -31.84 | -80.16 | -71.97 | 51.67 | -77.93 |
| 9.00 | 20.00 | 66.03 | -12.24 | -49.04 | -37.95 | 26.58 | -95.59 |
| 10.00 | 0.00 | 0.00 | 0.00 | -37.87 | 0.00 | 0.00 | -101.73 |
| 11.00 | 20.00 | 66.03 | -12.24 | -49.04 | -37.95 | 26.58 | -95.59 |
| 12.00 | 40.00 | 120.77 | -31.84 | -80.16 | -71.97 | 51.67 | -77.93 |
| 13.00 | 60.00 | 154.53 | -64.61 | -124.45 | -98.61 | 73.99 | -50.86 |
| 14.00 | 80.00 | 160.64 | -113.48 | -171.95 | -115.31 | 92.55 | -17.66 |
| 15.00 | 100.00 | 136.40 | -177.78 | -211.24 | -120.70 | 106.86 | 17.66 |
| 16.00 | 120.00 | 83.51 | -253.01 | -231.55 | -114.79 | 116.90 | 50.86 |
| 17.00 | 140.00 | 7.84 | -331.44 | -224.74 | -98.93 | 123.20 | 77.93 |
| 18.00 | 160.00 | -81.35 | -403.24 | -187.02 | -75.69 | 126.71 | 95.59 |
| 19.00 | 180.00 | -172.69 | -458.13 | -119.91 | -48.53 | 128.74 | 101.73 |
| MAX | 172.7 | 458.1 | 231.6 | 120.7 | 128.7 | 101.7 |
From the table above, it can be seen that the maximum internal forces occur when θ = 180°. Therefore, these values should be utilized to provide the flexural, shear and torsional reinforcement required in the helicoidal staircase.
See below for spreadsheet showing full analysis and design.
See: Designing a Concrete Spiral Staircase to EC2 | Worked Example
Sources & Citation
- Bergman, V.R (1956) “Helicoidal Staircases of Reinforced Concrete”, ACI Journal, 28, 403-412.
- Morgan, V.A. (1960) “Comparison of Analysis of Helical Staircases”, Concrete and Constructional Engineering (London), 55, 127-132.
- Santathadaporn, S., Cusens, A.R. (1966) “Charts for the design of Helical Stairs with Fixed Support” Concrete and – Constructional Engineering, 46-54.
- Reynolds, C.E., Steedman, J.C. (1988) “Reinforced Concrete Designer’s Handbook”, Tenth Edition, E. & F.N. SPON (London & Newyork), 386-391.
- Amin, A.F.M.S and Ahmad, S. (1998). An Economic Design Approach for Helicoidal Stair Slabs Based on Finite Element Analysis. 10.4203/ccp.56.6.4
Can you explain me how k’ factor came in output
Hi. This ia a very good guide on the design of helicoidal staircase, it has really helped me. However, I am a bit confused; On the question, β=360° ϕ=20° while on your calculations β=180° ϕ=25°. Please explain why. Thank you in advance
Can we adopt the same approach in designing RC.Helical Stringer beams,either centrally or on opposite edges of the stairway