Design of Pile Caps to Eurocode

Introduction

The concept of pile foundation is incomplete without discussing pile caps because the loads from the superstructure of a structure cannot be transferred directly on piles as it is most unlikely that a vertical within the superstructure will require a single pile to support the applied loads. It is common, however, to use piles in group, hence in order to distribute the load on the pile group, a pile cap is usually provided on the pile group, thereby efficiently transmitting the loads from the superstructure into the piles.

This article concerns the design of pile caps for a small group of piles, between 2-4 piles and purely axially loaded. It doesn’t consider large pile group and pile caps subjected to horizontal loads and/or moments due to the complexity in obtaining the load distribution of the pile group and the influence of differential settlement which further complicates their design. However, guidance on this aspect of pile caps can be obtained from the reference and further reading section of the article.

Pile Cap Design

The layout of the pile group is largely determined from the magnitude and location of actions they are to support from the superstructure. They are grouped together based on the pile’s capacity to support axial forces that can be either tension or compression, depending on the direction of the axial forces induced into the pile-cap from actions generated by the superstructure.

For simplicity, the location of piles with reference to the point of axial force application should be symmetrical. The proximity of piles to one another should be at least 3 × diameter of the pile. For pile-caps with 1 or 2 piles, some restraint needs to be provided orthogonally to the pile(s), which is usually achieved via ground beams. Figure 1 provides guidance on the location of piles in 2, 3 and 4 pile pile-caps where s is the spacing between piles.

Shows the setting out of piles within a pile cap — *Figure:1 Setting out of piles within 2, 3 and 4 pile-cap*

Determining axial forces in piles within pile-caps

When a pile cap is supporting an axial force N that is placed within the centroid of the pile group, the axial force in each pile is defined as:

\frac { N }{ n }

Where: n is the number of piles.

This only applies to piles within a pile group with at most 5 piles. Larger pile groups are subjected to large differential settlement and this tend to affect the force distribution between piles within the group. In most instances, the layout of the piles and the stiffness of the pile-cap plays a critical role in the force distribution, for example piles located closer to the centroid will be exposed to higher forces than those at the perimeter.

Design of Tension Reinforcement

Two methods of design are common: the beam theory and the strut &tie approach. In the former case the pile cap is treated as an inverted beam and is designed for the usual conditions of flexure and shear. The strut-tie assumes the reinforcement within the pile-cap is acting as if it were part of a truss, with the compression stresses being withstood by the concrete and the tension by the steel reinforcement. This method is applicable for pile-caps with less than 6 piles and is in fact the approach being considered for pile cap design in this article.

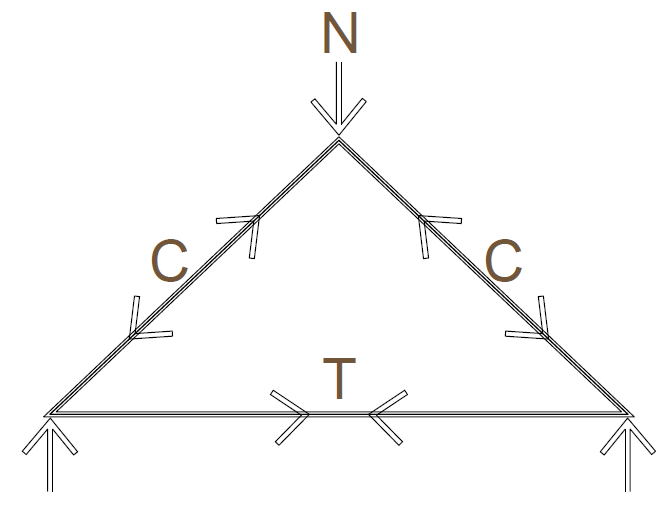
Truss analogy for pile cap design — *Figure 2: Truss action within a pile-cap showing compression strut*

Figure 2 shows the forces that pass through a pile-cap into the piles and how the strut and tie method is applied to it. It indicates how the depth of the pile-cap determines the magnitude of the forces within the concrete and the tension reinforcement. Typically the angle of the truss is set at 45º, which is then used to determine the depth of the pile-cap. Further iterations of this angle may be necessary as the size of the pile-cap is altered and/or the element it is supporting is modified to overcome geometry constraints and other extraneous design criteria. This can result in having a shallower angle that increases the tension in the reinforcement – as does the compression stress in the struts within the pile-cap.

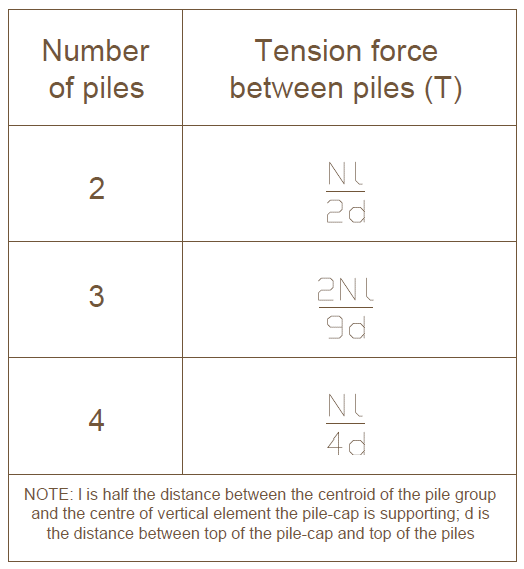
When the location of the axial force is not eccentric, the applied tension force between each pile can be calculated using table in figure 3

The tension reinforcement As required in the pile-cap is then defined as

{ A }_{ S }=\frac { T }{ 0.87{ f }_{ yk } }

Where: f_yk is the tension strength of the reinforcement, which is typically within the range of 400 – 500 N/mm2.

Shows the tensile force between piles in a typical 2, 3 and 4 pile cap — *Figure 3: Tensile force between piles*

Design of Shear Reinforcement

A critical shear plane adjacent to the vertical element that the pile-cap is supporting needs to be checked to determine whether or not it fails in shear. The plane’s location is based on the distance a_v, which is the dimension from the face of the vertical element the pile-cap is supporting and the face of a pile plus 0.2 × the pile diameter. This plane’s location is further explained in Figure 4. The shear verification is then carried out the same way we did for concrete beams.

Figure 4: Critical shear plane location in a 4 pile pile-cap

An additional check with respect to shear is required at the face of the vertical element the pile-cap supports.

{ N }_{ ED }<{ V }_{ RD,max }

Ned is the design axial load on the pile cap while VRd,max is the maximum shear resistance defined as

{ V }_{ RD,max }=0.2\left[ 1-\frac { { f }_{ ck } }{ 250 } \right] { f }_{ ck }pd

p is the perimeter length of the vertical element of the superstructure
d is the depth of the pile-cap

Pile Caps Reinforcement Detailing

There are several unique detailing requirements that are specific to pile caps. The anchorage length of the tension reinforcement is dependent on the bond conditions between the concrete and the steel. In the case of pile-caps, a good condition bond requires the reinforcement to be located within the 250mm depth of the concrete pour. For anything placed outside of that zone, the bond is considered to be ‘poor’. For more information on this see Clause 8.4.2 in BS EN 1992-1-1. The table provided in figure 5 shows the anchorage lengths for reinforcement bars based on concrete strength and bond conditions. A more accurate tension reinforcement anchorage length can be calculated using the guidance provided in Clause 8.4.3 of EN 19921-1. The minimum diameter of reinforcement used in a pile-cap is 8mm

*Figure 5: Typical anchorage length of tension bars in pile-caps*

Also, the minimum area of steel as defined for slabs & beams should also be verified to ensure that it is not critical

Worked Example

A 600×600 concrete column carries an axial design action of 4250 kN. Design a 4 pile pile-cap to support the column. The piles are 500mm in diameter cylindrical concrete. Design the pile cap completely using C30/37 concrete with 500mpa high tensile steel assuming the column to be placed in the centroid of the pile group.

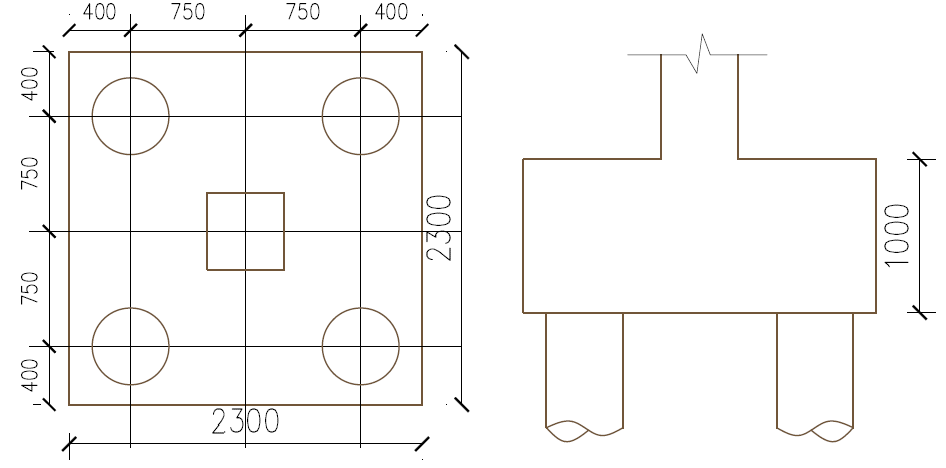
Geometry of the pile-cap

Try an overall depth h=1000mm with an average effective depth of 900mm, the spacing between piles = 3×500=1500mm and assuming an overhang of 400mm both ways. width of pile cap = 400+1500+400 = 2300mm. Figure 4 shows the trial geometry of the pile cap.