Derivation of Wind Loads to ASCE Code for Buildings

In this article, we explore the step-by-step process of deriving wind loads according to ASCE 7-22. The discussion includes theoretical insights, equations, and a detailed worked example to illustrate practical applications.

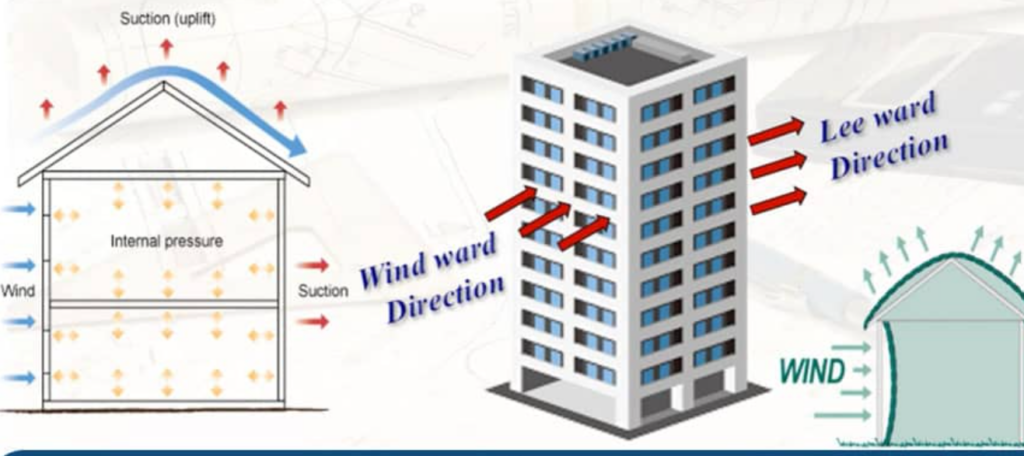
Structural design demands a thorough understanding of various environmental forces, with wind loads being one of the most critical considerations. Wind forces directly impact a building’s stability, safety, and functionality, making their accurate estimation essential. The consequences of misjudging wind forces can range from structural damage to catastrophic failures, endangering lives and property. This is why engineers rely on established standards, like the American Society of Civil Engineers (ASCE) 7-22 Standard, to derive wind loads effectively and ensure the integrity of buildings.

The ASCE 7-22 Standard, titled Minimum Design Loads and Associated Criteria for Buildings and Other Structures, provides a systematic approach to calculating wind loads. By factoring in elements such as terrain, building configuration, height, and risk categories, it enables engineers to design structures capable of withstanding extreme wind events. This standard is crucial in modern construction practices, offering precise guidelines that account for environmental variables and structural requirements.

In this article, we explore the step-by-step process of deriving wind loads according to ASCE 7-22. The discussion includes theoretical insights, equations, and a detailed worked example to illustrate practical applications. By the end, readers will gain a comprehensive understanding of the wind load calculation process, enhancing their ability to apply these principles in real-world scenarios.

Deriving Wind Loads to ASCE Code

1. Determine Basic Wind Speed

The first step in wind load derivation involves identifying the basic wind speed (V_ult), which reflects the intensity of wind forces in a given location. This parameter serves as the foundation for all subsequent calculations. ASCE 7-22 provides wind speed maps that indicate the fastest 3-second gust speeds measured at 33 feet above ground level in Exposure C terrain. These wind speeds correspond to a 50-year return period, representing the probability of encountering extreme wind events.

The basic wind speed varies significantly by region, influenced by geographic and climatic conditions. For instance, coastal areas prone to hurricanes may have much higher wind speeds than inland regions with milder weather patterns. Engineers must consult these maps to determine the appropriate wind speed for their project site, ensuring the structure is designed to withstand potential wind loads.

2. Identify the Risk Category

ASCE 7-22 assigns structures to one of four Risk Categories based on their purpose and the consequences of failure. This classification system ensures that structures serving critical functions or hosting large numbers of people are designed with higher safety margins.

• Category I: Includes structures with minimal hazard to human life, such as barns, storage units, or agricultural buildings.
• Category II: Encompasses most residential and commercial buildings. These are standard structures where failure would cause moderate risks.
• Category III: Covers buildings where failure could result in significant loss of life or property, such as schools, auditoriums, and large public facilities.
• Category IV: Applies to essential facilities like hospitals, fire stations, and emergency response centers, which must remain operational during disasters.

Each Risk Category has an associated importance factor (III), which modifies the basic wind speed. For example, essential facilities in Category IV have a higher importance factor to account for their critical role during emergencies.

3. Select the Exposure Category

The exposure category determines how terrain affects wind speeds near the structure. It accounts for variations in terrain roughness and obstacles that influence wind flow. ASCE 7-22 defines three exposure categories:

• Exposure B: Found in urban or suburban areas with dense buildings, which reduce wind speeds by creating turbulence.
• Exposure C: Typical of open terrain with scattered obstructions, such as fields or low-density residential areas.
• Exposure D: Represents flat, unobstructed areas near large water bodies, such as coastal zones, where wind speeds are highest.

Choosing the correct exposure category is critical because it directly impacts the calculated wind pressures on the structure.

4. Compute Velocity Pressure (q_h)

Velocity pressure quantifies the dynamic pressure exerted by wind on a structure at a specific height. It is a critical parameter in determining wind loads. The equation for velocity pressure is:

q_h=0.00256\cdot K_z \cdot K_{zt}\cdot K_d \cdot V^2 \cdot I

Where:

• K_z​: Velocity pressure exposure coefficient, which varies with height and exposure category.
• K_zt: Topographic factor, adjusting for features like hills or ridges.
• K_d: Directionality factor, accounting for the likelihood of wind approaching from specific directions.
• V: Design wind speed (V_ult).
• I: Importance factor from the Risk Category.

This equation highlights how terrain, building height, and wind speed influence wind pressure on a structure.

5. Determine Pressure Coefficients

Pressure coefficients (Cpe and Cpi​) account for wind interactions with the building’s surfaces and internal spaces.

• External Pressure Coefficient (Cpe​): Represents the effect of wind on a building’s exterior surfaces. It is derived from ASCE 7-22 tables and varies based on the structure’s shape, roof slope, and orientation.
• Internal Pressure Coefficient (Cpi​): Accounts for airflow inside the building due to openings, such as doors, windows, or vents.

Different building configurations—enclosed, partially enclosed, or open—have unique sets of pressure coefficients, reflecting their distinct airflow dynamics.

6. Calculate Wind Pressure (p)

Wind pressure on a surface is calculated as:

p=q_h \cdot(C_{pe}-C_{pi})

This equation combines the velocity pressure with external and internal pressure coefficients, providing a net wind pressure for specific surfaces. Calculating wind pressures accurately ensures the structure can withstand varying wind directions and intensities.

7. Combine Wind Loads with Other Loads

ASCE 7-22 emphasizes combining wind loads with other forces like dead, live, and snow loads to simulate real-world conditions. These load combinations are detailed in Section 2.3 of the standard, providing engineers with guidelines to follow when handling multiple forces simultaneously.

Worked Example

Consider a 15-story office building located in an area classified as Exposure C, with a flat roof and no significant topographical features. The building has a height of 180 feet and dimensions of 60 feet by 180 feet. The basic wind speed (V_ult) at the site is 150 mph, and the structure is classified as Risk Category II, with an importance factor (III) of 1.0. The goal is to calculate the wind loads acting on the structure, taking into account the velocity pressure, pressure coefficients, and the building’s dimensions. All calculations follow the ASCE 7-22.

Velocity Pressure Coefficients

• K_z=1.21 (from ASCE 7-22 Table 26.10-1 for 180 ft height).
• K_zt=1.0K_{zt} = 1.0Kzt​=1.0 (flat terrain).
• K_d=0.85K_d = 0.85Kd​=0.85 (standard for buildings).
• I=1.0 (Risk Category II).

Calculate Velocity Pressure (q_h)

q_h=0.00256\cdot K_z \cdot K_{zt}\cdot K_d \cdot V^2 \cdot I

q_h=0.00256\times1.21\times1.0\times0.85\times150^2\times 1.0 \\=58.9psf

Pressure Coefficients

• Windward Cpe=+0.8
• Leeward Cpe=−0.5
• Internal Cpi=±0.18

Net Wind Pressures

Windward

p_{windward}=q_h \cdot(C_{pe}-C_{pi})

=58.94\times(0.8-0.18) = 36.5psf

Leeward

p_{leeward}=q_h \cdot(C_{pe}-C_{pi})

=58.94\times(-0.5-0.18) = -40.1psf

Net Wind Load

For a building area of 60ft×180ft

• Windward Area: 10,800 ft²
• Leeward Area: 10,800 ft²

Net wind load:

P_{net}=(36.5\times 10800)+(-40.1\times10800) \\=-38.23lbs

Conclusion

Deriving wind loads as per ASCE 7-22 involves a systematic process that integrates multiple factors. From determining basic wind speed to calculating net pressures, each step plays a vital role in ensuring the safety and stability of structures. The worked example illustrates the application of these principles, offering practical insights into the design process.

See: Derivation of Wind Load to Signage Structures | Worked Example

Sources & Citations

• American Society of Civil Engineers (ASCE). Minimum Design Loads and Associated Criteria for Buildings and Other Structures (ASCE 7-22). Reston, VA: ASCE, 2022.
• Chowdhury, I., & Dasgupta, S.. Wind Loads on Buildings and Structures: Applications of the ASCE Standards. New York, NY: Springer, 2020.
• Holmes, J. D. Wind Loading of Structures. 4th ed. Boca Raton, FL: CRC Press, 2019.