Structural Analysis of Free-Standing Staircases | Worked Example

This article explores the analysis of free-standing staircases. It provides a comprehensive review of different analytical approaches for analyzing free-standing staircases and introduces a simplified method suitable for preliminary analysis and design.

Free-standing staircases, sometimes recognized as floating or cantilevered staircases, have surged in popularity within modern architectural designs owing to their captivating aesthetic appeal and efficient space-saving features. These staircases seemingly defy gravity, creating a captivating focal point in any space. Free-standing staircases are not just desired for their aesthetic appeal, they are often necessitated. Why? Conventional staircase is designed to have landing beams. However, these landing beams are not possible sometimes due to lack of columns supports or space constraints, necessitating the need for the landing to be suspended.

In terms of structural analysis, a free-standing staircase is just as complicated as the analysis of the helical staircases. While simple staircases type such the dogged leg, half and quatre turn all have code provisions and recommendation, in the instance of free standing and helical staircases, the codes are silent. Hence, the analysis and design of free-standing staircase has been based on rigorous analysis and there is no guideline regarding their analysis.

This article explores the literatures on the structural analysis of free-standing staircases and a simplified method for preliminary assessment and design purposes.

Structural Analysis Methods

In analyzing a free-standing staircase, several internal forces come into play, therefore the interaction between these forces must be considered. Several researchers have put forward analytical and numerical analysis concepts that can be used to make conservative designs. Some of these methods, many of which are based on the ‘strain energy concept’ are briefly discussed below.

Cussens and Kuang (1965)

The authors made the assumption that analyzing a free-standing staircase involves reducing the plate to beam elements. Consequently, the staircase takes the form of a space frame with beams positioned coincidentally with their longitudinal axes. The analysis relies on applying certain assumptions and the method of least work. The principle of least work is a recognized and potent tool for resolving statically indeterminate structural problems, particularly in the case of a three-dimensional frame where members undergo torsional stresses, in addition to conventional bending and axial stresses.

Taleb’s method (1964)

The Taleb’s method is an analytical method. It is based on the principle of least work using equations of equilibrium of the entire stair and hence obtaining expressions directly for all redundant acting at the supports. These redundant are then utilized to obtain the design forces in the free-standing staircase.

In the plane of the flights shear, tension and compression are ignored and the load cases include symmetri­cally and unsymmetrically placed loads.

Please see the sources and citation section of this article, for more on this method.

Liebenberg Method (1960)

This method which is also an analytical approach is called the ‘method of space interaction of plates.’ It involves utilizing the extensional (membrane or planar) stiffness created by the interaction between stair flights and landings. The ‘points’ or ‘lines’ of intersection formed by landings, columns, walls, beams, and floor slabs are considered supports for the ‘secondary load-carrying system’ handling bending stresses in slab elements. At the intersection points, extensional or membrane forces generate reactions that counterbalance the shear forces within the slab elements. The analytical procedure succinctly summarizes these steps.

1. First the conditions for a proper function of the primary system must exist. The effective supports are provided to the secondary bending system and local direct forces due to applied loading when inclined to the axis of the stair.
2. A provision of imaginary external restraints at supports thus preventing displacements and rotations.
3. Calculations of the resultant reactions acting on the imaginary supports.
4.  Determination of the magnitude of the forces in the primary system and the actual stresses due to the combined effect of the forces on both primary and secondary systems.

See the sources and citation section of this article, for more on this method.

Siev’s method (1983) 

The space interaction of plates forms the basic theory of analyzing stair­cases while assuming they are statically determinate. The plates are divid­ed into various horizontal shapes looking like trusses placed horizontally. The analysis is similar to that used in hipped plates. The line of the in­tersection between the flights and the landing is considered as a support and the load acting on it is resolved into forces in planes of the plates. Figures 2.5 and 2.8 show the various effects under symmetrical and antisymmetric loadings. This method is very similar to Liebenberg’s. Here torsional moments are then calculated as those moments causing compatibility in deformation.

Reynold’s and Steedman (1988)

The work done by Roxy and Reynolds is a simplification of Cosens’s and Kuang who utilized strain-energy principles to establish relationships between the horizontal restraint force (H) and moment (M_o) at the mid-point of a free-standing stair. By simultaneously solving the two equations derived, one can substitute the obtained values of H and M_o into general expressions, enabling the determination of forces and moments at any point along a free-standing staircase.

In simplifying the fundamental equations, the subsidiary terms can be neglected, resulting in the expressions provided in Table 2.88. of (Reynolds’s reinforced concrete designers handbook) reproduced as Figure 1 in this article. These expressions directly yield values for H and Mo. A comparison of solutions obtained through these simplified expressions with those derived using Cusens and Kuang’s original expressions indicates negligible variations within the range encountered in concrete design.

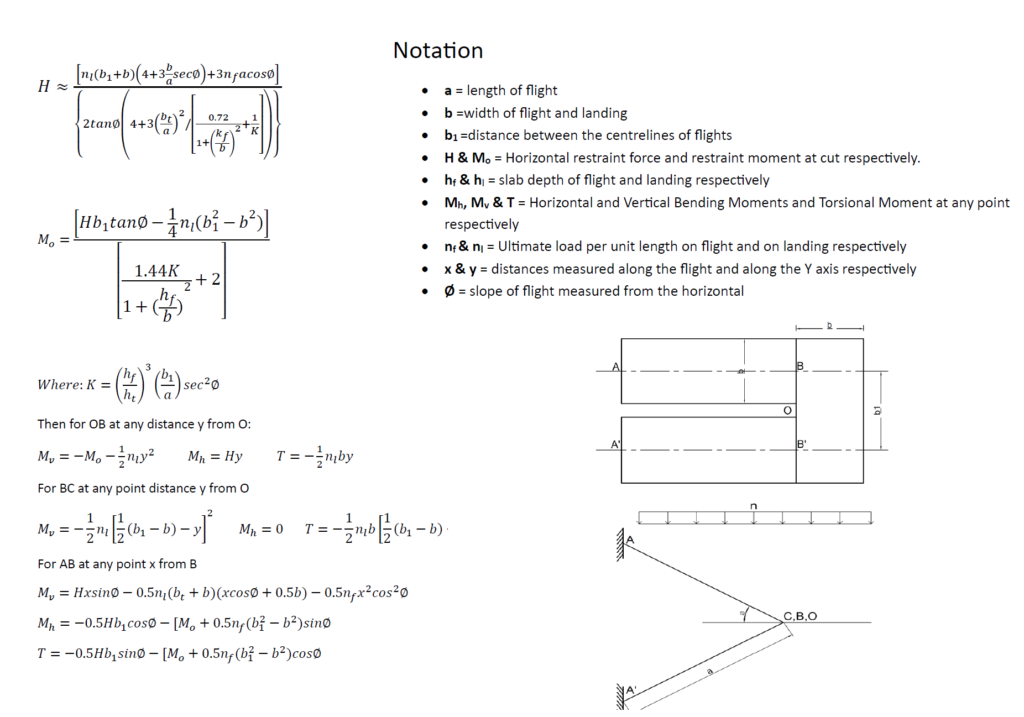
Note that these expressions are based on a value of G/E =0.4, with C taken as half of the St. Venant value for plain concrete. As assumed by Cusens and Kuang, only half of the actual width of the landing is considered to determine its second moment of area.

Finally, it must also be noted that, as with helical staircases, all analytical methods of analyzing free-standing staircases are flawed. This is because they are based on simplifications which fail cognize the distribution of stress resultant or the three-dimensional behaviour of the stair slab system. Hence, except for preliminary analysis and design, the finite element method is still the best approach to designing a free-standing staircase.

Worked Example

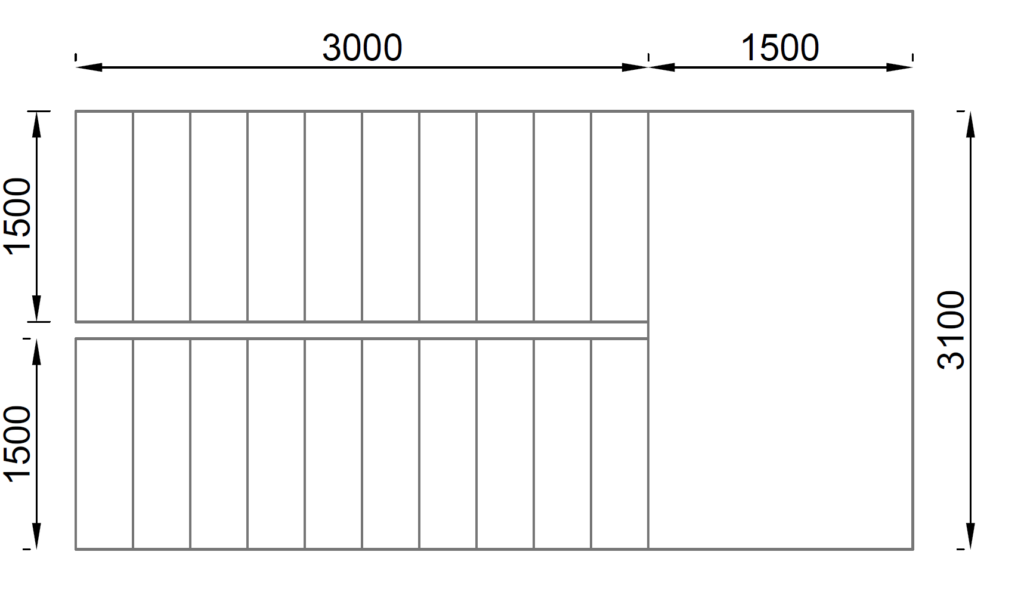
Figure 2 gives the geometry of a free-standing staircase required in a proposed commercial building. Assuming permanent action on the flight and landings are 9.5kN/m² and 4kN/m² respectively. Estimate the internal forces magnitude of the internal forces in the staircase. Note that the threads, riser and waist of the staircase is 300, 150 & 250mm respectively.

Actions

n_s =(1.35g_k+1.5q_k) \\=(1.35\times9.5+1.5\times4) \\=18.8kN/m^2

Geometry of Staircase

Slope of Flight

\phi =tan^{-1}\frac{1.5}{3} = 26.6^o

Length of flight

a=\sqrt{1.5^2+3^2} = 3.35m

Width of flight and landing

b = 1500mm

Distance between centerlines of flight

b_1= 1600mm 

Depth of flight and landing

h = 250mm

Analysis

If we apply the following parameters into the equation on Figure 1, we obtain the following values for K, H and M_o

K = 0.597

H = 292.5kN

M_o =  82.3kN.m

Having determined the values of Mo, H, these values can be substituted into the equations in Figure 1 to determine values for horizontal, vertical and torsional moment at any point x and y, and the maximum values utilized to provide the flexural, and torsional reinforcement required in the free-standing staircase.

Also See: Structural Design of Helicoidal Staircases | Worked Example

Sources & Citations

• Cusens, A. R., and Kuang, J. G, “Analysis of Free-Standing Stairs under Symmetrical Loading,” Concrete and Constructional Engineering, Vol. 60, No.5, 1965, pp. 167-172
• Taleb, N. J.: ‘The Analysis of Stairs with Unsupported Intermediate Landings,” Concrete and Constructional Engineering, Vol. 59, no.9 pp.315-320. 1964.
• Sieve, A., “Analysis of Free Straight Multiflight Staircases,” Journal of the Structural Division, ASCE, Vol.88, ST3, Proc. Paper 3168, 1962, pp.207-232.
• Reynolds, C. E. and Steedman, J. C., Reinforced Concrete Designer’s Handbook Eleventh Edition, E & FN Spon, London, 2008.
• Bangash, M. Y. H. and Bangash T., Staircases: structural analysis and design. A.A. Balkema, Rotterdam, 1999.