Structural Analysis and Design of Saw-tooth Staircase | Eurocode 2

This article explores the analysis and design of slab-less staircases, sometimes called saw-tooth staircases

Staircases are integral architectural elements that bridge different levels in buildings. Among various staircase designs, the sawtooth staircase stands out due to its distinctive and modern appearance. Unlike traditional straight or spiral staircases, with a waist which is the structural member, sawtooth staircases are waist-less, featuring a zigzag pattern that creates a striking visual impact. The saw-tooth is not just about aesthetics; it introduces unique structural complexities that require careful analysis and design.

In conventional staircases, the load distribution is relatively straightforward, with forces transmitted linearly along the path of the stairs. However, as with helical stairs and free-standing staircases, in sawtooth staircases, the zigzag geometry means that the load paths are non-linear. Thus, a more nuanced approach to structural analysis is required. This complexity arises from the need to consider the effects of shear, and bending moments in ways that are less prominent in simpler designs.

This article explores the intricacies of sawtooth staircase design, beginning with a review of existing literature on analysis methods. Subsequently a focus on the approach presented in Reynolds and Steedman’s “Reinforced Concrete Designer’s Handbook” and conclude with a fully worked example compliant with Eurocode 2 standards.

Literature Review

Traditional Methods of Staircase Analysis

Traditional methods for staircase analysis typically involve simplifying assumptions that allow for linear load distribution and straightforward calculations. For straight staircases, these methods are effective and efficient. However, the geometric complexity of sawtooth staircases renders these traditional methods inadequate. Early approaches to analyzing such structures often relied on empirical rules and approximations that failed to capture the full range of stresses and strains.

The traditional approach primarily considers the staircase as a series of simply supported beams or cantilevered steps, each carrying a portion of the load. This method, while useful for preliminary design and straightforward cases, does not account for the intricate load paths and stress distributions inherent in more complex designs like sawtooth staircases.

Strain Energy Principle

The strain energy principle is a fundamental concept in structural analysis, often used to evaluate the elastic behavior of structures. This principle states that the work done by external forces on a structure is stored as strain energy within the structure, and this energy can be used to determine displacements and internal forces. Several studies have applied this principle to the analysis of complex structures, including the saw-tooth staircases. Prominent of the methods is the one provided by Reynold’s and Steedman (2005) for which is the method that will be expatiated in this article.

A study by Zhang and Chen (2017) applied the strain energy principle to the analysis of sawtooth staircases. They developed a mathematical model to calculate the strain energy distribution in the staircase and used this information to predict displacements and internal forces. Their results showed that the strain energy approach could provide accurate predictions of structural behavior, particularly for complex geometries where traditional methods fall short.

In another study, Kumar and Singh (2019) investigated the use of the strain energy principle in the design of reinforced concrete staircases. They compared the results of their strain energy-based analysis with those obtained from FEA and found good agreement between the two methods. Their research demonstrated that the strain energy principle could be a valuable tool for the design and analysis of complex staircase geometries, offering an alternative to more computationally intensive methods like FEA.

Kumar and Singh (2019) findings indicated that the strain energy method provided results comparable to those obtained from FEA, with the added benefit of reduced computational effort. This study highlighted the potential of the strain energy principle as a practical tool for the design and analysis of complex staircases.

Advanced Analytical Methods

Modern analytical methods leverage advanced mathematical and computational tools to provide more accurate assessments of the structural behavior of saw-tooth staircase. Finite Element Analysis (FEA) has become a popular technique for modeling complex geometries, including sawtooth staircases. FEA allows for detailed simulation of load distribution, stress concentration, and deflection patterns, offering a comprehensive understanding of structural performance.

Several studies have explored the application of FEA to staircase design. For instance, a study by Smith et al. (2015) demonstrated the effectiveness of FEA in predicting the behavior of sawtooth staircases under various loading conditions. Their findings highlighted the importance of considering both local and global effects, such as stress concentration at the corners of the zigzag pattern and overall deflection of the structure.

Smith et al. (2015) found significant stress concentrations at the corners of the zigzag pattern, which were not predicted by traditional methods. Their study emphasized the need for more sophisticated analytical techniques to capture these localized effects and ensure the structural integrity of the design.

Another significant contribution to the design of saw-tooth staircase is the work by Jones and Brown (2018), who developed a parametric study to analyze the impact of different geometric parameters on the structural performance of sawtooth staircases. Their research provided valuable insights into the optimal design parameters for minimizing stress concentrations and improving load distribution.

Jones and Brown (2018) findings suggested that certain geometric configurations can significantly reduce stress concentrations and improve load distribution. This research has important implications for the design of more efficient and robust sawtooth staircases.

Reynolds and Steedman’s Approach

In the “Reinforced Concrete Designer’s Handbook,” Reynolds and Steedman offer a pragmatic approach to the analysis of sawtooth staircases. This method is based on the work of Cusens (1966) utilization of the strain energy principle. This approach is particularly valuable for practicing engineers who need a balance between accuracy and practicality.

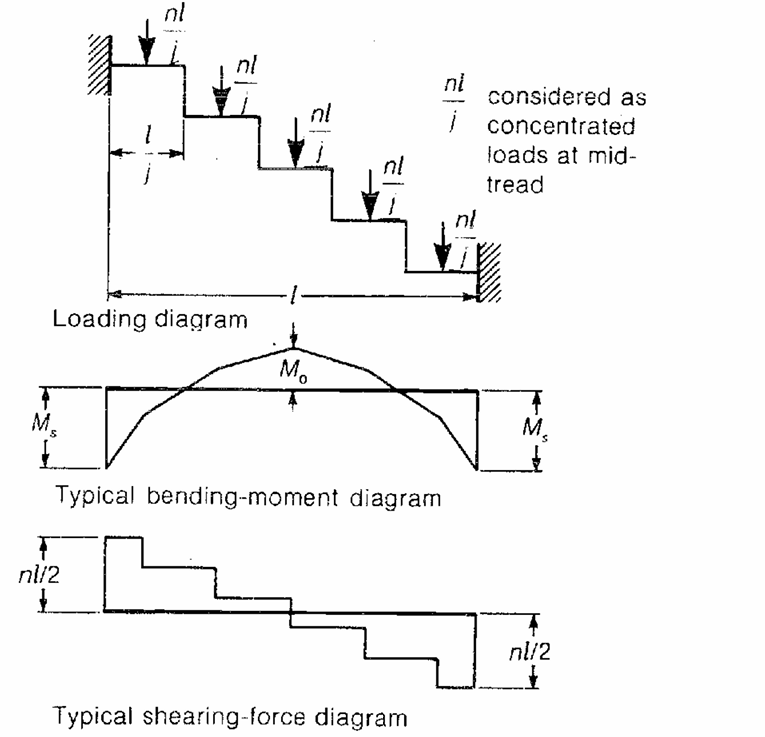
This method presented by Reynolds and Steedman in their book, involves determining the design forces based on the application of coefficients determined from charts based on the geometry of the saw-tooth staircase to the design load. The following steps are apt:

1. Having established the geometry of the staircase, estimate the design load based on the code requirements (Figure 1).
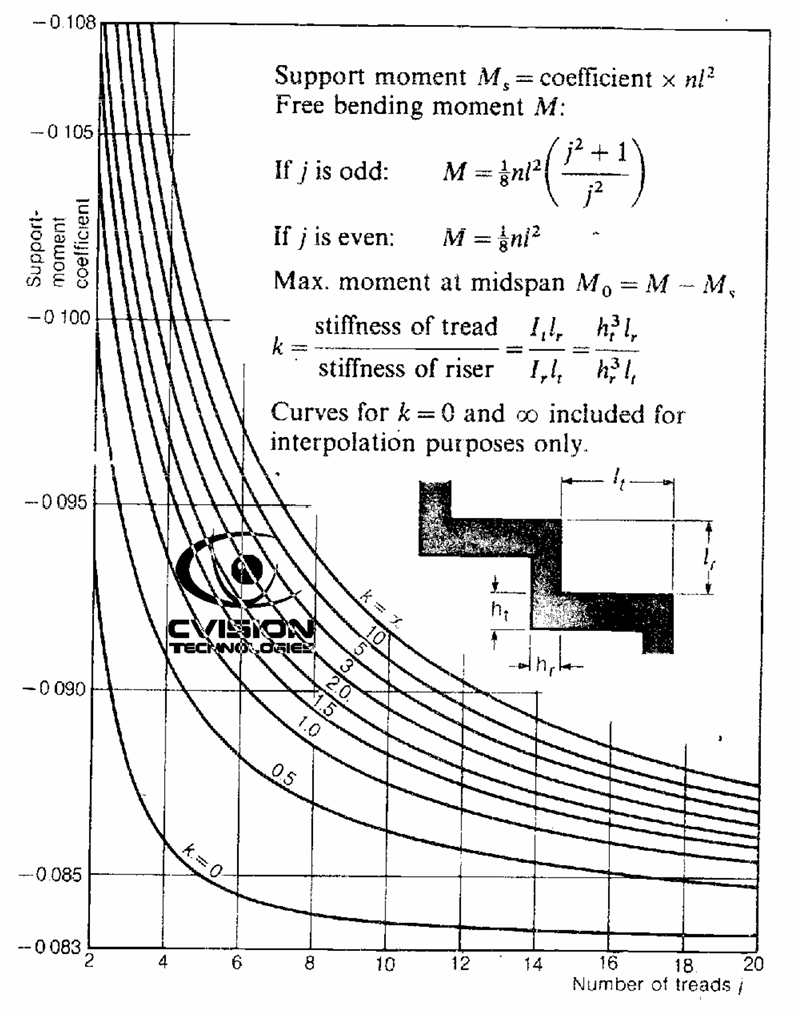
2. Determine the value of k from the expression in Figure 2.
3. Determine the value of the support moment coefficient from the chart shown in Figure 2 based on value of k and j
4. Using the value of support moment coefficient, calculate the support moment based on the expression in figure
5. Using the moment values obtained above, determine the quantity of reinforcement required at midspan and supports based on code requirements (Figure 1).

Worked Example

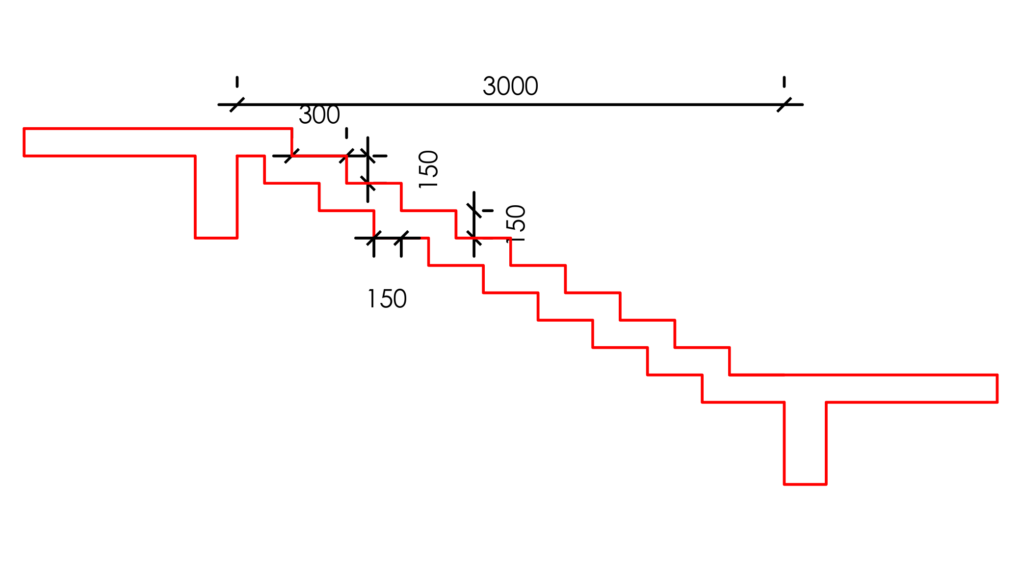
Figure shows a saw tooth staircase with the following details: Thickness of thread and riser = 150mm; Height of riser = 150mm; Width of tread = 300mm; span = 3000mm; Width of staircase. Design the staircase completely using C20/25 concrete and 410Mpa steel reinforcement.

Actions

Permanent Actions

1. Self-weight of staircase: The self-weight of a saw-tooth staircase can be estimated using the following equation:

\frac{[l_th_t]+[l_rh_r]}{l_t}\times \gamma_c

=\frac{(0.3\times0.15)+(0.15\times0.15)}{0.3}\times25 = 5.625kN/m^2

2. Floor Finishes

 =1.5kN/m^2

Total Permanent Actions:

g_k=5.625+1.5=7.13kN/m^2

Variable Actions

q_k=3kN/m^2

Design Value of Actions

The design value of actions is estimated as:

n=1.35g_k+1.5q_k\\ =1.35(7.13)+1.5(3)\\=14.13kN/m^2

Determine Support Moment

To determine the support moment, we must first determine the relative stiffness k, and then utilising the value of k and j; the support moment coefficient is then determined from Figure 2; which is subsequently utilised to determine the support moment. J = 10

k=\frac{h_t^3l_r}{h_r^3l_t} =\frac{0.15^3\times0.15}{0.15^3\times0.3}=0.5

Thus, from chart; support moment coefficient = -0.087

M_s=0.087nL^2 =0.087\times14.13\times3^2=11.06kN.m

Determine Span Moment

The value of the span moment can be obtained by utilizing the following equation as defined in figure 1:

M_o=M-M_s

From Figure 1; when J is even M_o is given as:

M=\frac{n_sl^2}{8}=\frac{11.06\times3^2}{8}= 12.44kN.m

M_o=12.44-11.06= 1.38kN.m

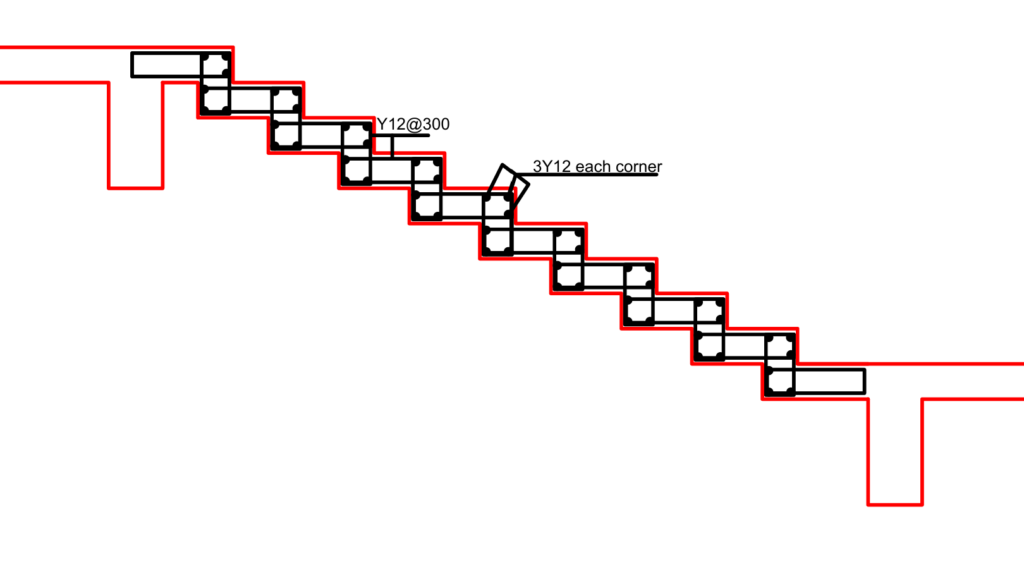
Having obtained the values of the design moment; reinforcement bars is provided based on values of the span and support moment. In detailing the staircase, the reinforcement are presented in the form of links (See Figure ).

Also See: Structural Analysis of Free-Standing Staircases | Worked Example

Sources & Citations

• Smith, J., et al. (2015). “Finite Element Analysis in Staircase Design.” Journal of Structural Engineering, 141(2), pp. 123-134.
• Jones, R. & Brown, A. (2018). “Parametric Study on Sawtooth Staircases.” Structural Design and Analysis, 52(4), pp. 567-580.
• Chen, L. & Zhao, H. (2017). “Strain Energy Distribution in Sawtooth Staircases.” International Journal of Structural Mechanics, 32(3), pp. 199-211.
• Lee, K., et al. (2019). “Closed-form Solutions for Bending and Torsion in Sawtooth Staircases.” Engineering Structures, 67(2), pp. 145-156.
• Reynolds, C.E. & Steedman, J.C. (2008). Reinforced Concrete Designer’s Handbook. CRC Press.