Impact of Settlement on Internal Stresses in Structures

This article explores the impact of settlement on structures, particularly how it impacts design internal forces.

Settlement in structures refers to the downward movement of a building or a part of a building as a result of soil compression. This phenomenon can cause significant changes to the internal stresses in a structure. When parts of the foundation settle unevenly, it induces differential movement. This can create additional bending moments, shear forces, and axial forces. Such additional stresses may exceed the design capacity of structural members, leading to cracking, excessive deflection, or even failure.

Settlement is a normal process in all structures to some degree. It becomes problematic when differential settlement occurs—when different parts of the structure settle at different rates or to different extents. The additional forces generated from this uneven settlement impose unexpected loads on the structure, requiring designers to account for them in the design process.

This article explores the subject of settlement and the impact it has on internal stresses of structures.

Types of Settlement

There are various ways settlement can manifest, with two key forms being uniform and differential settlement.

Uniform Settlement

Uniform settlement happens when the entire foundation of a building sinks at a consistent rate. While it may result in a slight downward movement of the building, this type of settlement generally does not lead to significant structural stress, as the movement is evenly distributed across all parts of the building. However, uniform settlement can still pose issues related to the connection of the building to external utilities, such as pipes and conduits, which may not be able to tolerate even minor shifts in position.

Differential Settlement

In contrast, differential settlement occurs when different parts of a building settle at different rates or to different extents. This form of settlement is much more dangerous because it introduces distortions within the structure, placing unexpected loads on the beams, columns, and foundation. The stresses caused by differential settlement often exceed the capacities of structural members, leading to a range of issues from cracks and deformations to severe structural failures.

Tipping settlement is even a more extreme case of differential settlement, where one side of the building settles at a much faster rate than the other, causing the building to tilt. This can lead to large bending moments and shear forces in both the foundation and the superstructure.

Effects of Settlement on Internal Stresses

The internal stresses in a structure are significantly affected by settlement, particularly when it is uneven. The bending moments, shear forces, and axial forces that develop within structural elements, such as beams and columns, are directly impacted by differential settlement. When part of the foundation settles unevenly, beams spanning across settled and unsettled areas are subjected to additional bending. The change in support conditions causes the beam to bend and deform in ways that were not anticipated in the original design, leading to increased bending moments.

Beams are especially vulnerable to differential settlement. When the supports of a beam shift unevenly, the beam is forced to accommodate the movement by bending. In a well-designed structure, the bending moments in the beams are calculated based on static loads and the assumption that supports remain fixed. However, when one end of a beam settles while the other remains fixed, additional moments are introduced. These moments increase the stresses within the beam and can lead to cracking, excessive deflection, or even failure if the beam is not capable of resisting the increased loads.

Columns, too, are affected by settlement. When settlement occurs, particularly differential settlement, columns experience changes in their alignment. Columns are generally designed to carry vertical loads, and any lateral or diagonal movement caused by settlement introduces additional forces that must be resisted. In some cases, the axial forces within the columns increase due to the settlement, placing additional stress on the column. If the column is not adequately designed to handle these forces, it may buckle or crush, especially if the column is slender and more prone to instability.

Worked Example: Impact of Settlement on Internal Forces

To demonstrate the impact of settlement, in this example, we will calculate the additional forces generated in a beam – column frame due to settlement and the percentage increase in the design forces.

Problem Statement

A fixed frame structure consists of a horizontal steel beam with a length of 6 meters and two vertical steel columns, each with a height of 3 meters, supporting the beam (Figure 1). The beam is subjected to a uniformly distributed load of 15 kN/m, and the moment of inertia of the beam section is 2844 × 10⁻⁶ m⁴, while the columns have a cross-sectional area of 0.01156 m² and a moment of inertia of 20300 × 10⁻⁶ m⁴. The material of the members has a modulus of elasticity E of 210 GPa. Assuming the left column supports experiences a vertical differential settlement of 75 mm. Estimate the Increase in the internal forces a result of this change.

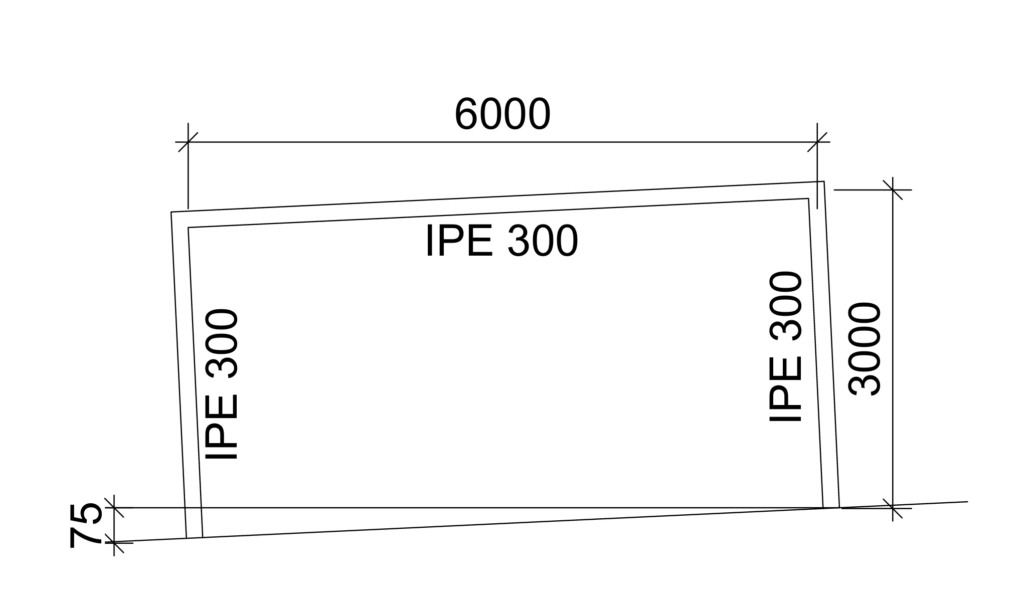
Bending Moment in Beams and Columns

Without Settlement (Initial Condition)

Assuming a fixed ended connection between the columns and the beam; maximum support moment is given as:

M=\frac{wl^2}{12}=\frac{15\times6^2}{12}=45kN.m

With Settlement

The differential settlement of one support induces additional moments in the beam and columns due to the rigid connections at the joints. The additional moment caused by the support settlement can be approximated by:

M_{\delta}=\frac{6EI\delta}{l^2}

=\frac{6\times210\times10^3\times2844\times10^{-6}\times0.075}{6^2} =12.44kN.m

Thus, the total moment in the beam after settlement is:

M_{total}=M_o+M_{\delta}= 45+12.44= 57.44kN.m

Similarly, the additional moment in the column base is assumed to be approximately equal to the induced moment in the beam:

M_{col} =12.44kN.m

Shear Force in Beams and Columns

Without Settlement (initial condition)

The shear force at the supports due to the uniformly distributed load is:

V_0=\frac{wl}{2}=\frac{15\times6}{2}=45kN

With Settlement

The additional shear force due to the settlement can be approximated by:

V_{\delta}=\frac{6EI\delta}{l^3}

=\frac{6\times210\times10^3\times2844\times10^{-6}\times0.075}{6^3} =2.1kN

Thus, the total shear force in the beam supports after settlement is:

V_{total}=V_0+V_{\delta}=45+2.1=47.1kN

Axial Force in Columns

Without Settlement (initial condition):

The axial force in each column before settlement is equal to the reaction from the beam load:

P_0=\frac{wl}{2}=\frac{15\times6}{2}=45kN

With Settlement:

The additional axial force due to the settlement is caused by the vertical displacement and can be calculated as:

P_{\delta}=\frac{EA_c\delta}{h}

=\frac{210\times10^3\times0.01156\times0.075}{3} =60.7kN

Thus, the total axial force in the left column (the one with settlement) is:

P_{l,total}=P_0+P_{\delta}=45+60.7=105.7kN

Similarly, the axial force in the right column (no settlement) will experience a net-tension

P_{l,right}=P_0-P_{\delta}=45-60.7 =-15.7kN

Percentage Increase in Forces

Bending Moment:

\frac{M_{\delta}}{M_{0}} =\frac{12.33}{45}= 27.65\%

Shear Force:

\frac{V_{\delta}}{V_{0}} =\frac{2.1}{45}= 4.62\%

Axial Force:

\frac{P_{\delta}}{P_{0}} =\frac{60.7}{45}= 135\%

Summary of Results

• Bending moment in the beam increased by 27.65%.
• Shear force in the beam increased by 4.62%.
• Axial force in the left column increased by 134.87% due to the settlement.

Design Considerations for Settlement

To mitigate the effects of settlement, structural engineers must consider the potential for uneven foundation movement during the design process. The only way to mitigate against the effect of settlement is to limit settlement. One way of doing this is by using deep foundations, which extend into more stable soil layers below the surface. These foundations transfer the load of the building to deeper strata that are less likely to compress, reducing the risk of differential settlement. This approach is particularly useful in areas where the surface soils are soft or prone to compression.

Another strategy to reduce the impact of settlement is to use raft or mat foundations. A raft foundation spreads the building’s load over a larger area, minimizing the stress on any one point of the foundation. By distributing the load more evenly, a raft foundation reduces the risk of differential settlement and helps to maintain the stability of the structure. In cases where differential settlement is expected, settlement joints can be used. These joints allow different sections of the building to move independently of each other, reducing the internal stresses that arise from uneven settlement.

Monitoring systems can also be used to detect settlement early and allow for timely intervention. By installing sensors in the foundation and structure, engineers can track the movement of the building over time. If settlement is detected, corrective actions, such as underpinning or soil stabilization, can be taken to prevent further movement. Monitoring systems are particularly valuable in buildings constructed on soils that are known to be prone to settlement, as they provide real-time data on the performance of the structure.

Also See: Settlement of Bored Pile Foundations |Worked Example

Conclusion

Settlement, particularly differential settlement, not only affects sub-structures but has a profound impact on the internal stresses within a structure. Beams and columns experience significant increases in bending moments, shear forces, and axial forces due to uneven foundation movement. And the worked example demonstrates how these forces can be significant.