This article explores how engineers idealise structures for analysis. It explains what idealisation involves, how to classify structural elements, and how to model boundary conditions
Every structural engineer begins with a concept. Before applying any calculations or detailing drawings, they must first visualise how a structure will behave. This visualisation is not a casual sketch but a refined process that transforms architectural ideas into workable engineering systems. Engineers must consider how the structure carries gravity, wind, seismic, and imposed loads. They must determine which elements act together and which remain independent. These decisions form the core of structural idealisation.
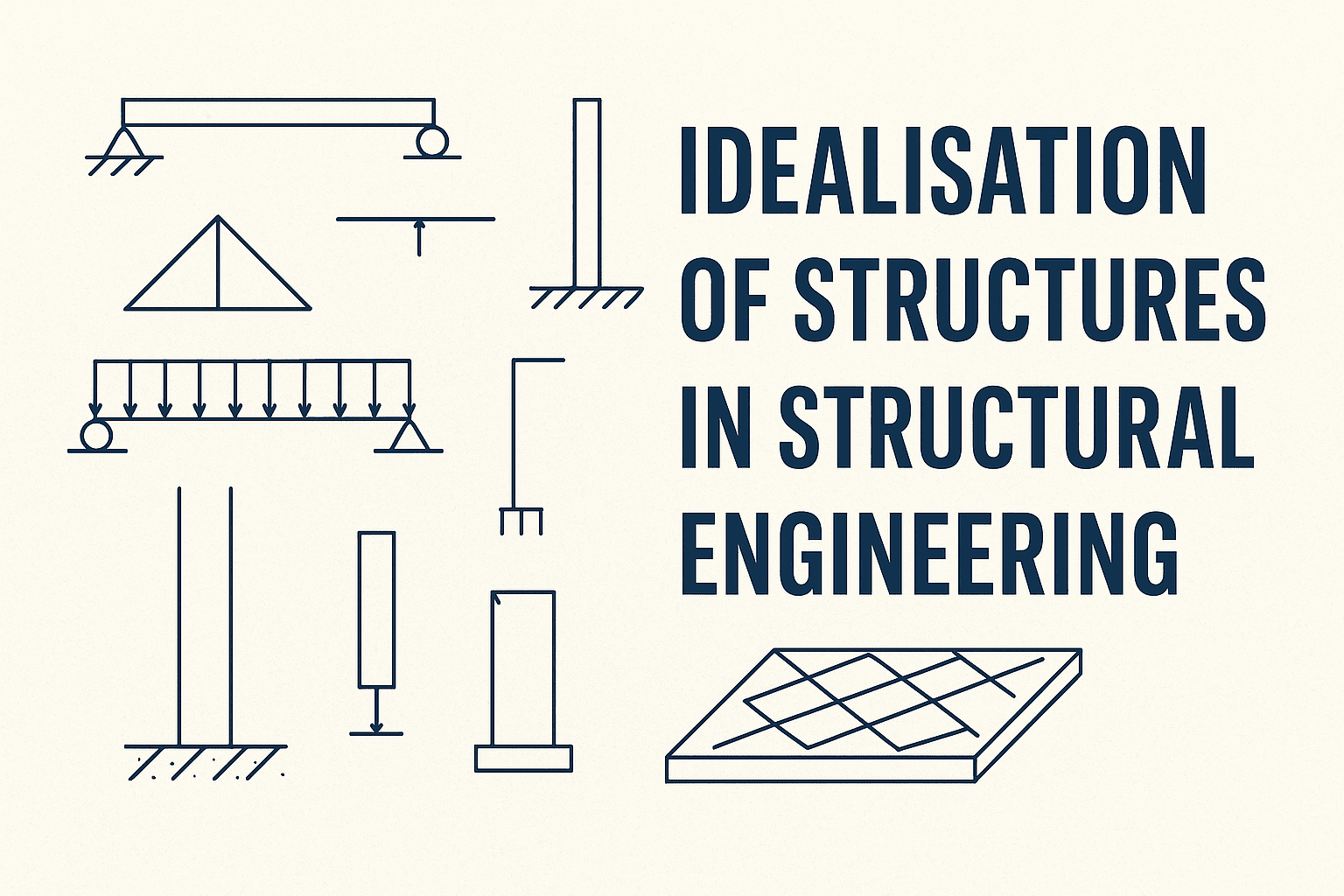
Idealisation means reducing complex, real-world forms into simplified, analyzable systems. These simplified systems mimic how the structure behaves under load. Engineers use this concept to break down entire buildings, bridges, or tanks into smaller, mathematically predictable components. Without this abstraction, analysis becomes impossible, no matter how advanced the tools. Idealisation allows engineers to move from a raw architectural form to a logical model they can verify against code provisions.
This article explores how engineers idealise structures for analysis. It explains what idealisation involves, how to classify structural elements, and how to model boundary conditions. The article discusses how simplifications affect accuracy and how engineers judge what assumptions are safe. It covers both manual and software-based modelling and aims to clarify the balance between simplification and realism.
What is Structural Idealisation?
Structural idealisation involves representing a physical structure with a simplified model that behaves similarly under loading. Engineers do not need to copy every wall, bolt, or slab thickness in their minds or models. Instead, they abstract the system into representative components. These components have idealised geometry, support conditions, connections, and materials.
The goal is not to replicate the exact physical reality. Rather, it is to develop a mathematical model that captures the main structural actions. This model should include only the necessary complexity to deliver safe and reliable analysis results. Idealisation allows the structure to be interpreted in terms of internal forces, deflections, stresses, and failure modes.
In simple terms, idealisation helps engineers focus only on the essential structural behaviour. It excludes decorative elements, over-detailed joints, and non-contributing masses. In most cases, idealisation defines how beams, slabs, walls, and supports interact. This enables the application of known analytical tools such as stiffness matrices, influence lines, or moment distribution methods.
Why Idealisation is Necessary
Real structures contain infinite complexities. If engineers tried to model every bolt hole, temperature variation, and material grain, analysis would become impossible. Even with powerful software, complete modelling remains inefficient and unnecessary. Idealisation trims away unnecessary details and focuses on what matters for stability, strength, and serviceability.
Idealisation also helps engineers interpret code requirements. Building codes expect engineers to use design load paths, idealised supports, and simplified shapes. Most code provisions rely on textbook assumptions. For instance, the design moment in a slab assumes idealised boundary conditions and material properties. Without idealisation, applying such formulas becomes meaningless.
Another key benefit of idealisation lies in communication. Engineers must communicate their models to clients, drafters, reviewers, and contractors. A clear, simplified structural model helps align understanding across the project team. This consistency ensures that the design intent translates correctly from concept to drawings to construction.
Basic Components in Idealised Structures
Structural idealisation begins by identifying the primary load-carrying components. These include:
1. Beams and Girders
These elements support loads along their length and transfer them to supports or columns. Engineers idealise beams as line elements with flexural, shear, and sometimes axial capacity.
2. Columns
Columns carry axial loads and sometimes bending. They are idealised as vertical line elements that transfer load to the foundation.
3. Slabs and Plates
Slabs distribute loads to beams or walls. Engineers idealise them as 2D plate elements, either acting in one direction or two.
4. Shear Walls and Core Walls
These resist lateral loads such as wind or seismic forces. Engineers model them as planar vertical elements fixed at the base.
5. Foundations
Footings and piles support vertical and horizontal forces. They are idealised as point or line supports with translational and rotational stiffness.
6. Bracing and Frames
These resist lateral forces and maintain overall stability. They are often modelled as axial-only members or rigid connections.
Each component receives a simplified representation that allows calculation of internal actions such as moments, shears, axial forces, and deflections.
Types of Structural Systems in Idealisation
The structural form dictates how engineers idealise it. The main types of structural systems include:
1. Load-Bearing Wall Systems
These use walls to carry vertical loads. Idealisation focuses on vertical wall elements transferring loads to footings. Openings reduce effective stiffness and must be modelled accordingly.
2. Moment Resisting Frames
These use beam-column connections to resist lateral loads. Engineers model each connection’s moment continuity. The frame is treated as an indeterminate system with rigid joints.
3. Braced Frames
These include diagonal members that resist lateral loads in trusses or rigid frames. Engineers idealise bracings as axial-only elements and model their buckling potential.
4. Shear Wall Systems
These provide lateral resistance through wall panels, often with vertical and horizontal reinforcement. Idealisation includes in-plane shear deformation and boundary element strength.
5. Flat Slab Systems
These transfer loads directly to columns without beams. Engineers model slabs as plates and pay special attention to punching shear at column interfaces.
6. Truss Systems
These include members connected at pinned joints to form triangulated frames. Engineers idealise them as axial-only elements with zero bending.
Each system demands a different approach to idealisation depending on its load transfer mechanism, geometry, and redundancy.
Idealising Supports and Boundary Conditions
One of the most critical steps in structural idealisation is defining boundary conditions. Supports determine how the structure resists movement. Misrepresenting supports leads to grossly incorrect results.
Common Support Types:
- Pinned Support: Allows rotation but resists translation in both directions. Ideal for simple beams or hinge connections.
- Fixed Support: Resists translation and rotation. Used in wall bases, deep pile caps, and rigid frames.
- Roller Support: Resists vertical load but allows horizontal movement. Used in expansion joints or long-span decks.
When idealising supports, engineers also account for foundation flexibility. In real structures, soil deformation affects base stiffness. Advanced idealisation includes spring supports to reflect subgrade reactions or pile group behaviour.
Engineers must also model continuity. A slab that continues into a wall or beam behaves differently than a slab with an edge drop. Failing to capture this continuity may lead to underestimated moments or cracking.
Idealisation of Connections and Joints
Joints connect individual structural components. The way they behave influences how forces flow through the structure. In idealisation, joints are usually classified as:
- Pinned: No moment transfer, only axial and shear force.
- Rigid: Full moment continuity, no relative rotation between members.
- Semi-Rigid: Partial moment transfer, based on rotational stiffness.
Correct joint idealisation allows realistic frame behaviour under load. For instance, misclassifying a semi-rigid joint as fully rigid may overestimate moment resistance. Connection types must match detailing plans, including bolt patterns, welds, and plates.
Engineers may idealise frame joints as hinges or fixed based on material, loading, and intended performance. In software, joint rotational stiffness can be numerically adjusted to simulate realistic response.
Material Idealisation
Engineers do not only idealise geometry but also materials. They idealise materials using stress-strain relationships, modulus values, and strength capacities. For concrete, linear elastic models apply until cracking. For steel, bilinear idealisation captures elastic and plastic behaviour.
Simplifying assumptions include:
- Homogeneous and isotropic materials.
- Linear elasticity before ultimate load.
- Perfect bond between reinforcement and concrete.
These assumptions simplify analysis but introduce limitations. Engineers must adjust results using partial safety factors or crack control provisions. In nonlinear or performance-based design, material idealisation becomes more advanced, using plasticity, creep, and time-dependent factors.
Modelling Techniques in Structural Idealisation
Engineers apply idealisation using both manual and software-based approaches. In manual analysis, simplified methods include:
- Tributary area calculations for loads.
- Moment distribution for continuous beams.
- Frame analysis using shear-moment diagrams.
In software (ETABS, SAP2000, STAAD, RFEM), engineers construct idealised models using:
- Line elements for beams and columns.
- Shell elements for slabs and walls.
- Springs and dampers for supports or damping.
- Rigid links to simulate stiff connections.
For both methods, idealisation must balance simplicity and realism. Over-simplification may ignore crucial behaviours, while over-complexity may lead to incorrect interpretation. Engineers rely on experience, verification, and code guidance to make decisions.
Examples of Common Structural Idealisations
Let us examine a few everyday examples of structural idealisation:
1. Multi-Storey Concrete Building
- Columns: line elements carrying axial and moment loads.
- Beams: rigidly connected line elements.
- Slabs: idealised as rigid diaphragms or shell elements.
- Core walls: planar vertical shell elements.
- Foundations: pinned or spring supports based on soil model.
2. Industrial Steel Portal Frame
- Rafters and columns: line elements with rigid joints.
- Bracing: axial-only elements for wind load.
- Base: pinned support with moment-resisting plinth.
- Purlins and sheeting: omitted from global model, included in secondary checks.
3. Bridge Deck with Box Girder
- Deck: shell elements for plate action.
- Girders: frame elements connected to diaphragms.
- Supports: roller and fixed bearings idealised with spring stiffness.
- Barrier and parapet loads included as surface pressures or line loads.
These examples show how idealisation allows complex systems to be simplified into analysable models while preserving core structural logic.
Limitations and Cautions in Idealisation
Idealisation always introduces approximations. If engineers simplify too aggressively, they risk omitting important behaviours. Common pitfalls include:
- Ignoring lateral-torsional buckling in slender beams.
- Assuming full moment continuity where the joint cannot transfer moments.
- Treating slabs as rigid diaphragms where they are not.
- Misrepresenting soil–structure interaction.
Engineers must validate their assumptions using checks, design experience, and code guidance. In some cases, they conduct sensitivity analyses using multiple idealisations. In others, they cross-verify global and local models to ensure alignment.
Documentation remains key. Engineers must explain their idealisation strategy in reports, drawings, and calculations. This transparency ensures that design reviewers and builders understand how decisions were made.
Conclusion
Structural idealisation forms the foundation of structural engineering analysis. It bridges the gap between architectural concept and engineering design. Idealisation allows engineers simplify complex systems into manageable components. These components form mathematical models that reflect real behaviour within safe limits.
The process involves representing beams, slabs, columns, supports, and connections in idealised forms. Engineers consider boundary conditions, continuity, and material properties. They balance simplicity with accuracy and apply the right level of complexity for each project.
Also See: Structural Design Guidelines and Methodology
Sources & Citations
- BS EN 1990:2002 – Eurocode: Basis of Structural Design
- Salmon, C. G., Johnson, J. E., & Malhas, F. A. (2008). Steel Structures: Design and Behavior (5th ed.). Pearson.
- Mosley, W. H., Bungey, J. H., & Hulse, R. (2012). Reinforced Concrete Design (7th ed.). Red Globe Press.
- Chopra, A. K. (2017). Dynamics of Structures: Theory and Applications to Earthquake Engineering (5th ed.). Pearson.