Fundamentals of Finite Element Analysis in Structural Engineering

In this article, we explore the principles, workflow, applications, and types of Finite element analysis in structural engineering.

Finite Element Analysis (FEA) is a transformative computational tool in structural engineering, widely used to predict the behavior of structures under various conditions. From bridges and skyscrapers to tunnels and foundations, FEA helps engineers design safe and efficient structures by simulating real-world scenarios.

In essence, FEA divides a structure into smaller, manageable parts called finite elements. These elements are analyzed individually, and their responses are combined to provide insights into the structure’s overall behavior. This method allows engineers to solve complex problems involving stresses, deformations, heat transfer, and vibrations with high precision.

FEA has revolutionized structural engineering by offering a way to test designs virtually before physical construction begins. It reduces costs, enhances safety, and optimizes material use. In this article, we explore the principles, workflow, applications, and types of FEA in structural engineering.

Why FEA is Important in Structural Engineering

Structural engineering focuses on designing structures that can safely withstand various forces and environmental conditions. Traditional methods of analysis often rely on simplifying assumptions, limiting their application to straightforward problems. FEA, however, eliminates these limitations by enabling the analysis of complex geometries, materials, and load conditions.

For instance:

• A high-rise building must withstand wind forces, seismic activity, and live loads from occupants. FEA allows engineers to evaluate all these factors simultaneously.
• In a bridge, FEA helps analyze stresses caused by traffic loads, thermal expansion, and environmental forces, ensuring a robust design.

By providing detailed insights into how a structure will perform, FEA helps engineers identify potential weaknesses, optimize designs, and ensure compliance with safety standards.

How FEA Works

At its core, FEA involves dividing a structure into smaller elements in what is called a mesh (Figure 1), which form a mesh. Each element is governed by mathematical equations that describe physical behavior, such as stress-strain relationships or heat conduction. These equations are solved numerically, and the results are combined to predict the structure’s overall performance.

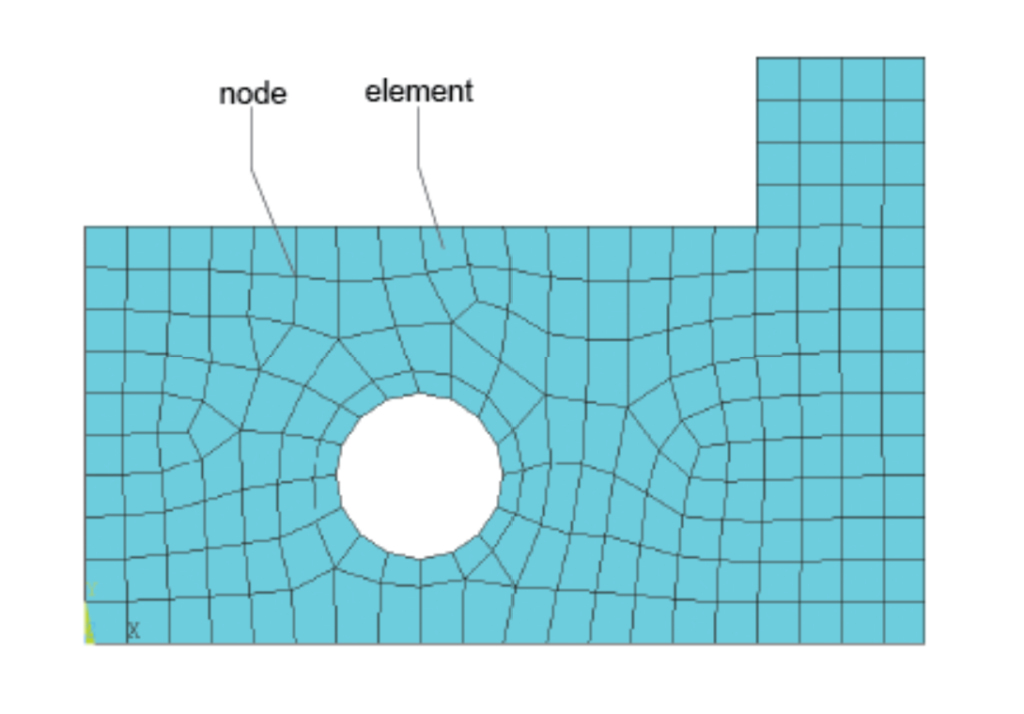
The process involves three main stages:

1. Pre-Processing: Preparing the model for analysis by defining its geometry, material properties, boundary conditions, and mesh.
2. Solution Phase: Solving the governing equations for each element and assembling the results.
3. Post-Processing: Visualizing and interpreting the results, such as stress distributions, deformation patterns, or reaction forces.

This structured approach makes FEA a versatile tool for addressing a wide range of structural challenges.

Key Steps in the FEA Process

As described above, key steps in the FEA process involves, pre-processing, solution phase and post-processing. This is explained in more details in the next sections.

Pre-Processing

The first step in FEA is defining the problem. Engineers create a digital model of the structure using CAD software or directly within the FEA platform. Key components of this phase include:

• Geometry Creation: The structure’s shape and size are modeled. For complex geometries, simplifications may be made to reduce computational effort without compromising accuracy.
• Material Assignment: Properties like elasticity, density, and thermal conductivity are specified. For example, a concrete bridge deck and steel reinforcement will have distinct properties.
• Boundary Conditions: Constraints (e.g., fixed supports) and external forces (e.g., wind or live loads) are applied to the model.
• Meshing: The structure is divided into finite elements. A finer mesh typically improves accuracy but increases computation time.

Pre-processing ensures the model accurately represents the real-world system, laying the foundation for reliable results.

Solution Phase

Once the model is prepared, the software solves the governing equations for each element. In structural engineering, these equations are derived from mechanics of materials and include relationships between forces, displacements, and material properties.

The solution phase involves:

• Calculating displacements at each node.
• Determining element stresses and strains from nodal displacements.
• Assembling these results to obtain the structure’s overall response.

Advanced solvers can handle various complexities, including nonlinear behavior, dynamic loads, and coupled phenomena like fluid-structure interaction.

Post-Processing

In this stage, engineers analyze the results to understand how the structure will behave under the applied conditions. Common outputs include:

• Stress Distribution: Identifies regions of high stress that may require reinforcement.
• Deformation Patterns: Shows how the structure will deform under loads, ensuring deflections are within acceptable limits.
• Reaction Forces: Verifies whether supports can handle the expected loads.

Post-processing tools provide visual representations, such as color-coded stress contours or animated deformation, making it easier to identify critical areas and refine designs.

Applications of FEA in Structural Engineering

1. Building Design

High-rise buildings and large complexes face diverse forces, from wind and seismic loads to occupant-induced vibrations. FEA helps engineers:

• Evaluate wind-induced sway and design damping systems.
• Analyze earthquake responses through time-history or modal analysis.
• Optimize structural systems for material efficiency while maintaining safety.

For example, FEA enables precise analysis of stress concentrations around openings like windows and doors, guiding reinforcement placement.

2. Bridge Engineering

Bridges experience dynamic and static forces from traffic, wind, and environmental conditions. FEA applications in bridge design include:

• Predicting fatigue life of critical components under repeated loading.
• Analyzing cable forces and deck deformations in suspension and cable-stayed bridges.
• Assessing stability and resonance under pedestrian or vehicle-induced vibrations.

3. Foundation Engineering

Foundations must transfer loads from structures to the ground safely and efficiently. FEA aids in:

• Studying soil-structure interactions, including settlement and lateral pressures.
• Designing pile foundations for optimal load distribution.
• Evaluating the effects of varying soil conditions, such as liquefaction in seismic zones.

This analysis helps engineers choose the most suitable foundation type and dimensions.

4. Rehabilitation and Retrofitting

Existing structures often require evaluation for safety or upgrading to meet modern standards. FEA plays a critical role in:

• Assessing the structural integrity of aging buildings and bridges.
• Simulating retrofitting measures, such as adding braces or applying fiber-reinforced polymers.
• Analyzing the impact of modifications on overall stability and load distribution.

By offering detailed insights, FEA supports efficient and effective rehabilitation efforts.

Types of FEA Analyses

FEA encompasses various types of analyses tailored to specific problems:

Linear Static Analysis

This is the simplest form of FEA, assuming small deformations and linear material behavior. It is suitable for static loads like gravity or wind on structures within their elastic limits.

Nonlinear Analysis

Nonlinear FEA accounts for:

• Large deformations.
• Nonlinear material behavior, such as plasticity in steel or cracking in concrete.
• Contact phenomena, like friction between structural components.

This analysis is essential for studying failure modes or post-yield behavior.

Dynamic Analysis

Dynamic FEA evaluates structures under time-dependent forces, such as:

• Vibrations caused by wind, earthquakes, or moving vehicles.
• Resonance effects in bridges or tall buildings.

It includes methods like modal analysis and time-history analysis, providing insights into natural frequencies and dynamic responses.

Thermal and Multiphysics Analysis

Although primarily used in structural contexts, FEA also addresses thermal effects, such as:

• Heat transfer in concrete during hydration.
• Thermal expansion in steel components.

Multiphysics FEA combines structural, thermal, and fluid analyses, offering comprehensive solutions for complex interactions.

Benefits of FEA in Structural Engineering

FEA offers several advantages that make it indispensable in structural engineering:

1. Precision: Provides detailed insights into stress, deformation, and load distribution.
2. Cost Savings: Reduces the need for physical prototypes and extensive testing.
3. Flexibility: Handles irregular geometries, complex materials, and multiple loading conditions.
4. Safety Assurance: Identifies weak points, ensuring designs meet safety standards and regulations.
5. Design Optimization: Enables engineers to refine designs for material efficiency and performance.

Challenges of FEA

Despite its advantages, FEA has limitations and challenges:

1. Modeling Accuracy: Inaccurate input data, such as material properties or boundary conditions, can lead to unreliable results.
2. Computation Time: Large models with fine meshes require significant computational resources, increasing analysis time.
3. User Expertise: Effective use of Finite element analysis demands a solid understanding of structural mechanics and numerical methods.
4. Validation Needs: Finite element analysis results must be validated with experimental data or simplified analytical solutions to ensure accuracy.

Future Trends in FEA for Structural Engineering

The field of FEA continues to evolve, with advancements enhancing its capabilities and accessibility:

1. Integration with AI and Machine Learning: Predictive modeling and optimization are becoming more efficient with AI algorithms.
2. Cloud Computing: Cloud-based FEA platforms offer scalability, enabling engineers to solve large models faster.
3. Real-Time Analysis: Innovations in computational power are enabling near-real-time simulations, improving decision-making during design processes.
4. Sustainability Focus: FEA is increasingly used to design energy-efficient structures and optimize material use for reduced environmental impact.

Conclusion

Finite Element Analysis (FEA) is a transformative tool in structural engineering, enabling precise analysis of complex structures under various conditions. By breaking structures into finite elements, FEA provides detailed insights into stresses, deformations, and other performance metrics, ensuring safe and efficient designs.

See: Common Errors in FEA and how to avoid them

Sources & Citations

1. Smith, J. (2018). Finite Element Methods in Structural Engineering. New York: Springer.
2. Brown, R., & Lee, M. (2020). “Advanced Applications of FEA in Bridge Design.” Journal of Structural Analysis, 45(3), 123-137.
3. International Federation of Structural Engineers (IFSE). (2019). Guidelines for FEA in Structural Design. Geneva: IFSE Publications.
4. Chen, P., & Kumar, A. (2021). “Nonlinear FEA for Seismic Retrofitting of High-Rise Buildings.” Engineering Structures, 89, 289-305.