Despite their importance, analyzing transfer slabs presents significant challenges due to their complex load distributions and interactions with supporting systems.

Transfer slabs are crucial elements in modern construction, particularly in high-rise and hybrid buildings where architectural and functional requirements often dictate structural irregularities. These slabs serve as horizontal load redistribution systems, bridging the discontinuities in load paths between different structural levels. By effectively transferring vertical loads to lower levels, transfer slabs ensure stability and allow for versatile architectural layouts. Their role is particularly significant in buildings where space constraints or mixed-use designs necessitate structural adaptations.
The necessity of transfer slabs arises from the need to accommodate changing column layouts or supporting systems between floors. In many cases, lower floors are designed for commercial use with large, open spaces, while upper floors house apartments or offices with different column arrangements. Without transfer slabs, maintaining structural integrity across such variations becomes challenging. These slabs not only redistribute loads but also enable creative architectural designs and optimized use of space.
Despite their importance, analyzing transfer slabs presents significant challenges due to their complex load distributions and interactions with supporting systems. These slabs often experience large bending moments, shear forces, and torsional stresses, especially in thick, column-supported configurations. Accurate analysis is essential to ensure safety and efficiency. However, the intricate behavior of these slabs often necessitates advanced modeling techniques and a deep understanding of structural mechanics.
Methods of Analyzing Transfer Slabs
Analyzing transfer slabs requires precise methods to account for load redistribution, stress distribution, and structural stability. These methods ensure safety, material efficiency, and compliance with design standards. The primary approaches include the Finite Element Method (FEM), Kirchhoff slab theory, the Hillerborg strip method, and yield line theory.
Kirchhoff Slab Theory
Kirchhoff slab theory, also known as classical plate theory, is a fundamental method for analyzing transfer slabs. It assumes the slab’s thickness is small compared to its other dimensions, typically less than one-fifth of its shortest span. This theory extends the principles of Euler-Bernoulli beam theory to two-dimensional plates, enabling the calculation of stress and strain distributions.
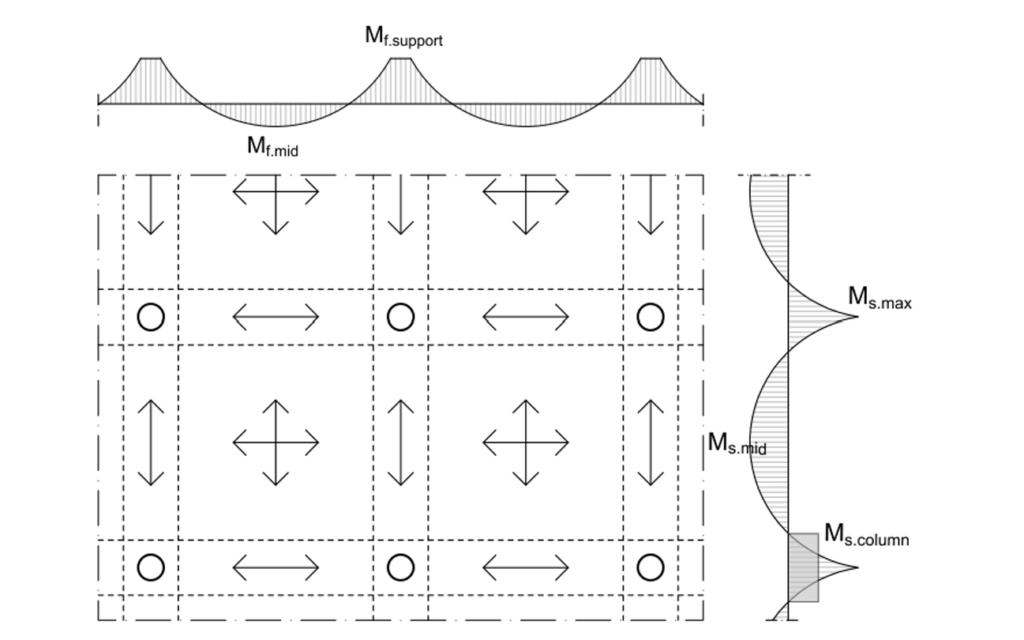
The key assumption in Kirchhoff slab theory is that normal material lines remain perpendicular to the slab’s mid-surface during deformation. Shear deformations are neglected, simplifying the analysis. Moments and shear forces are calculated using established formulas.
For example, the maximum moment at a column support (M,smax) is:
M_{s,max}=\frac{q\times L^2}{12}and the moment at midspan (Ms,mid) is:
M_{s,mid}=\frac{q\times L^2}{24}Here, q represents the uniformly distributed load, and L is the distance between supports. These calculations provide insights into moment distribution and help optimize reinforcement placement. Reinforcements are concentrated near areas of high stress, such as column tops and midspans, ensuring efficient use of materials.
While Kirchhoff theory is suitable for thin slabs with regular geometries, it has limitations in analyzing thick slabs or those with complex support conditions. For such cases, advanced methods like FEM are preferred to capture additional effects like torsion and large deformations.
Hillerborg Strip Method
The Hillerborg strip method applies principles of plasticity theory to determine the ultimate load-carrying capacity of transfer slabs. This method divides the slab into load-carrying strips aligned with the reinforcement, typically along column lines and midlines. The analysis is performed one direction at a time, simplifying the calculations for complex slabs.
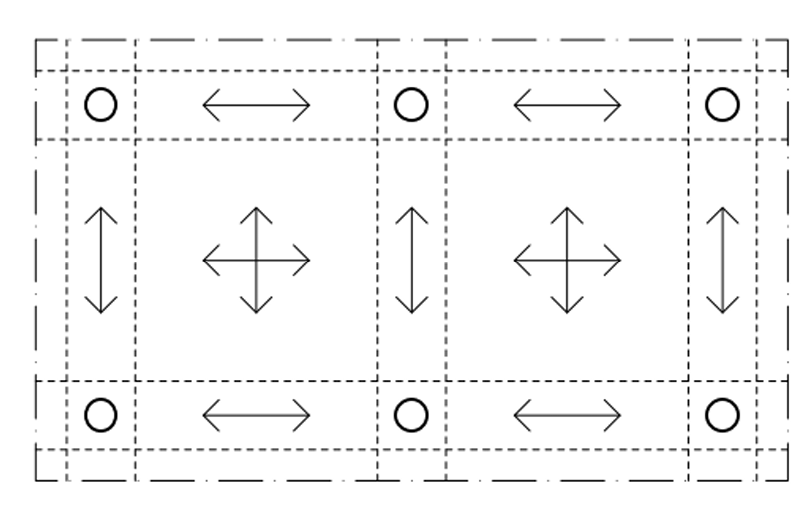
The method uses the lower-bound theorem, which states that as long as equilibrium is maintained and the yield criterion is not violated, the slab will not fail. Average support moments (ms) are calculated as:
m_s=\frac{qL}{14}and field moments (mf) are derived using:
m_f=\frac{q\frac{L}{2}^2}{2}-m_sThese moments are redistributed to reinforce critical areas, such as near column supports. The method is conservative, providing a safe estimate of the slab’s ultimate capacity. However, it may lead to over-reinforcement, increasing construction costs. Designers must balance safety with material efficiency when using this approach.
Yield Line Theory
Yield line theory estimates the upper limit of the load capacity by identifying likely failure lines. These lines indicate the slab’s critical cracking patterns under maximum loading. Using this method, moments at potential yield lines are calculated to define the slab’s load-carrying capacity.
Unlike other methods, yield line theory is less conservative and provides an overestimated load capacity. Its primary limitation lies in its reliance on designer assumptions to identify the correct yield lines, making it less reliable for complex geometries or load distributions.
Finite Element Method (FEM)
The Finite Element Method (FEM) is by far the most accurate method of analysing transfer slabs computational technique used to model and analyze complex transfer slabs. It divides the slab into smaller, discrete elements to create a computational model. Each element is evaluated for stresses, strains, and deformations based on the nodal displacements.
Using software such as RFEM, engineers simulate the structural behavior under various load conditions. The governing equations for FEM rely on the relationships between displacements and internal forces. For instance, the stiffness matrix, derived from material properties and geometry, calculates the nodal displacements that generate internal stresses.
FEM is especially beneficial for thick slabs, where manual calculations are challenging due to complex interactions between bending moments, shear forces, and torsional stresses. However, its accuracy depends on selecting appropriate boundary conditions, discretisation levels, and material models. Errors in these parameters can lead to incorrect assessments of load-carrying capacities and stress distributions.
Additional Considerations for Transfer Slab Analysis
Analyzing transfer slabs requires careful consideration of several additional factors. One critical aspect is the torsional moment, particularly in thick slabs. Ignoring torsion can lead to underestimating design moments, compromising structural safety. Including torsional effects ensures a more accurate representation of the slab’s behavior under complex loading conditions.
Punching shear strength is another vital consideration for column-supported transfer slabs. High stresses often concentrate at column-slab connections, leading to potential punching shear failures. The punching shear capacity of the slab without reinforcement is calculated using the basic control perimeter and additional reinforcement is required if this capacity is insufficient.
Deflection control is also essential to ensure serviceability. Excessive deflections can compromise the slab’s aesthetic and functional performance. Accurate modeling of load-deformation relationships is crucial, particularly for slabs with large spans or high loads. Serviceability Limit State (SLS) checks verify that deflections remain within acceptable limits.
Conclusion
Each method of analyzing transfer slabs has specific applications and limitations. FEM provides detailed stress analysis for complex slabs but requires expertise in modeling and software. Kirchhoff theory offers a simplified approach for thin slabs, while the Hillerborg strip method ensures safety through conservative designs. Yield line theory is efficient for determining load limits but may lack reliability for intricate slab designs. Selecting the appropriate method depends on slab geometry, loading conditions, and project requirements.
See: Design of Transfer Slabs: A Comprehensive Overview
Sources & Citations
- Tattari, Jonna. Optimized Design of a Load Transfer Concrete Slab. Master Thesis, Royal Institute of Technology (KTH), 2022.
- Enochsson, O., & Dufvenberg, E. (2001). “Finite Element Modeling for Thick Slabs.” In-depth study of FEM applications in slab design.
- Nilsson, O., Olofsson, K., & Jonasson, J. (2012). “Kirchhoff Slab Theory and Applications in Structural Engineering.” Essential reference for classical slab analysis approaches.
- Saarinen, M., & Kähkönen, T. (2013). “Hillerborg Strip Method for Reinforced Concrete.” Practical guide on using strip methods for slab designs.